题目
如果一个字符串不含有任何重复字符,我们称这个字符串为好字符串。
给你一个字符串 s ,请你返回 s 中长度为 3 的好子字符串的数量。
注意,如果相同的好子字符串出现多次,每一次都应该被记入答案之中。
子字符串是一个字符串中连续的字符序列。
示例 1:
输入:s = “xyzzaz”
输出:1
解释:总共有 4 个长度为 3 的子字符串:“xyz”,“yzz”,“zza” 和 “zaz” 。
唯一的长度为 3 的好子字符串是 “xyz” 。
示例 2:
输入:s = “aababcabc”
输出:4
解释:总共有 7 个长度为 3 的子字符串:“aab”,“aba”,“bab”,“abc”,“bca”,“cab” 和 “abc” 。
好子字符串包括 “abc”,“bca”,“cab” 和 “abc” 。
提示:
- 1 <= s.length <= 100
- s 只包含小写英文字母。
题解
长度为3,互不相同可以直接拿不等于进行两两判断
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int countGoodSubstrings(String s) {
if (s.length() < 3) return 0;
char[] str;
int n = 0;
for (int i = 0; (i + 3) <= s.length(); i++) {
str = s.substring(i, i + 3).toCharArray();
if (str[0] != str[1] && str[0] != str[2] && str[1] != str[2]) {
n++;
}
}
return n;
}
}
|
大聪明做法:如果子字符串的长度继续增加,可以考虑滑动窗口,当然每次遍历cnt数组还是有开销的
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public int countGoodSubstrings(String s) {
int len = s.length();
if(len < 3) return 0;
int res = 0;
int[] cnt = new int[26];
for(int i = 0; i < 3; i++){
cnt[(int)(s.charAt(i) - 'a')]++;
}
for(int i = 0; i < len - 3; i++){
if(isValid(cnt)) res++;
cnt[(int)(s.charAt(i) - 'a')]--;
cnt[(int)(s.charAt(i + 3) - 'a')]++;
}
if(isValid(cnt)) res++;
return res;
}
public boolean isValid(int[] cnt){
for(int x: cnt){
if(x > 1) return false;
}
return true;
}
}
|
题目
一个数对 (a,b) 的数对和等于 a + b 。最大数对和是一个数对数组中最大的 数对和 。
比方说,如果我们有数对 (1,5) ,(2,3) 和 (4,4),最大数对和 为 max(1+5,2+3,4+4)=max(6,5,8)=8 。
给你一个长度为 偶数 n 的数组 nums ,请你将 nums 中的元素分成 n / 2 个数对,使得:
nums 中每个元素 恰好 在 一个 数对中,且
- 最大数对和 的值 最小 。
- 请你在最优数对划分的方案下,返回最小的 最大数对和 。
示例 1:
输入:nums = [3,5,2,3]
输出:7
解释:数组中的元素可以分为数对 (3,3) 和 (5,2) 。
最大数对和为 max(3+3,5+2)=max(6,7)=7 。
示例 2:
输入:nums = [3,5,4,2,4,6]
输出:8
解释:数组中的元素可以分为数对 (3,5),(4,4) 和 (6,2) 。
最大数对和为 max(3+5,4+4,6+2)=max(8,8,8)=8 。
提示:
n == nums.length
2 <= n <= 10^5
n 是 偶数 。
1 <= nums[i] <= 10^5
题解
排序 + 贪心
猜测:将数组排序,前后组合即可
关键在于证明:
令当前数组有序,即x1≤...≤xn
考虑上述命题的充分条件:假设给定拆分方法中的数对和xk+xn+1−k 在 k=k′时最大,那么对于任意的拆分方法,都存在一组 u,v,使得 xu+xv≥xk′+xx+1−k′
反证法:
假设u<v,那么使得xv≥xn+1−k′的v值为闭区间
内部[n+1−k′,n]的所有整数,有k′种,如果想使xu+xv<xk′+xx+1−k′恒成立,必有xu<xk′,但是u的取值只有[1,k′−1],共k′−1种,两者数量不匹配,无法对于全部数对满足,故不成立,反证法得证
代码很简单如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public int minPairSum(int[] nums) {
int max = 0;
int len = nums.length;
Arrays.sort(nums);
int lo = 0, hi = len - 1;
while(lo < hi){
max = Math.max(nums[lo] + nums[hi], max);
lo++;
hi--;
}
return max;
}
}
|
类似题目: AcCoder Regular Contest 121
题目
给你一个 m x n 的整数矩阵 grid 。
菱形和 指的是 grid 中一个正菱形 边界 上的元素之和。本题中的菱形必须为正方形旋转45度,且四个角都在一个格子当中。下图是四个可行的菱形,每个菱形和应该包含的格子都用了相应颜色标注在图中。
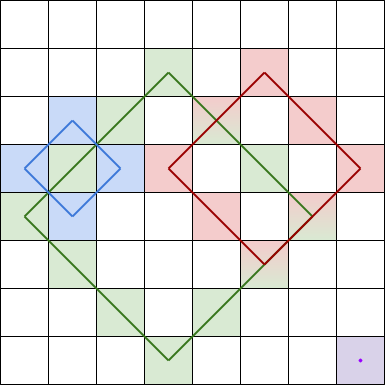
注意,菱形可以是一个面积为 0 的区域,如上图中右下角的紫色菱形所示。
请你按照 降序 返回 grid 中三个最大的 互不相同的菱形和 。如果不同的和少于三个,则将它们全部返回。
示例 1:

输入:
grid=[[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
输出:[228,216,211]
解释:最大的三个菱形和如上图所示。
蓝色:20 + 3 + 200 + 5 = 228
红色:200 + 2 + 10 + 4 = 216
绿色:5 + 200 + 4 + 2 = 211
示例 2:
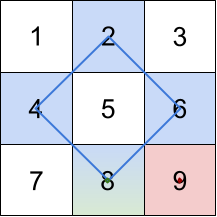
输入:grid=[[1,2,3],[4,5,6],[7,8,9]]
输出:[20,9,8]
解释:最大的三个菱形和如上图所示。
蓝色:4 + 2 + 6 + 8 = 20
红色:9 (右下角红色的面积为 0 的菱形)
绿色:8 (下方中央面积为 0 的菱形)
示例 3:
输入:grid=[[7,7,7]]
输出:[7]
解释:所有三个可能的菱形和都相同,所以返回 [7] 。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 100
1 <= grid[i][j] <= 10^5
题解
这道题目挺恶心,当场没做出来,暴力模拟即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| class Solution {
public int[] getBiggestThree(int[][] grid) {
int mm = grid.length;
int nn = grid[0].length;
List<Integer> list = new ArrayList();
int cur = 0;
for (int i = 1; i <= 50; i++) {
for (int x = i - 1; x < mm - i + 1; x++) {
for (int y = i - 1; y < nn - i + 1; y++) {
cur = 0;
for (int xx = x - i + 1; xx <= x + i - 1; xx++) {
cur += grid[xx][y - ((i - 1) - Math.abs(xx - x))];
if ((i - 1) - Math.abs(xx - x) != 0) {
cur += grid[xx][y + ((i - 1) - Math.abs(xx - x))];
}
}
list.add(cur);
}
}
}
HashSet set = new HashSet(list);
list.clear();
list.addAll(set);
Collections.sort(list);
int ans[];
if (list.size() >= 3) {
ans = new int[3];
ans[0] = list.get(list.size() - 1);
ans[1] = list.get(list.size() - 2);
ans[2] = list.get(list.size() - 3);
} else {
ans = new int[list.size()];
for (int i = 0; i < list.size(); i++) {
ans[i] = list.get(list.size() - i - 1);
}
}
return ans;
}
}
|
题目
给你两个整数数组 nums1 和 nums2 ,它们长度都为 n 。
两个数组的 异或值之和 为 (nums1[0]XORnums2[0])+(nums1[1]XORnums2[1])+...+(nums1[n−1]XORnums2[n−1]) (下标从 0 开始)。
比方说,[1,2,3] 和 [3,2,1] 的 异或值之和 等于 (1XOR3)+(2XOR2)+(3XOR1)=2+0+2=4 。
请你将 nums2 中的元素重新排列,使得 异或值之和 最小 。
请你返回重新排列之后的 异或值之和 。
示例 1:
输入:nums1=[1,2],nums2=[2,3]
输出:2
解释:将 nums2 重新排列得到 [3,2] 。
异或值之和为 (1XOR3)+(2XOR2)=2+0=2 。
示例 2:
输入:nums1=[1,0,3],nums2=[5,3,4]
输出:8
解释:将 nums2 重新排列得到 [5,4,3] 。
异或值之和为 (1XOR5)+(0XOR4)+(3XOR3)=4+4+0=8 。
提示:
n == nums1.length
n == nums2.length
1 <= n <= 14
0 <= nums1[i], nums2[i] <= 10^7
题解
这题看到n≤14问题就很简单了,套用一个状压dp,创建数组dp[len+1][1<<len]
dp[i][j]表示nums1数组前i−1个元素与nums2对应二进制j状态量之间的最优解
为了规范边界条件,我们设定dp[0]该行表示nums1数组前0个元素的对应取值,即全为0
我们得到转移方程
dp[i][j]=Math.min(dp[i−1][j−(1<<k)]+(nums1[i−1]⨁nums2[k]),dp[i][j])
其中k为状态量j的1所在的位数, 则j−(1<<k)表示为j状态去除一个元素后的状态
注意加法和异或的优先级问题
代码如下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
public int minimumXORSum(int[] nums1, int[] nums2) {
int len = nums1.length;
int[][] dp = new int[len + 1][1 << len];
for(int[] x: dp) Arrays.fill(x, Integer.MAX_VALUE / 2);
Arrays.fill(dp[0], 0);
for(int i = 1; i <= len; i++){
for(int j = 0; j < (1 << len); j++){
int tmp = j;
int cnt = 0;
while(tmp != 0){
tmp &= tmp - 1;
cnt++;
}
if(cnt != i) continue;
for(int t = 0; t < len; t++){
if((j & (1 << t)) != 0){
dp[i][j] = Math.min(dp[i - 1][j - (1 << t)] + (nums1[i - 1] ^ nums2[t]), dp[i][j]);
}
}
}
}
return dp[len][(1 << len) - 1];
}
}
|














