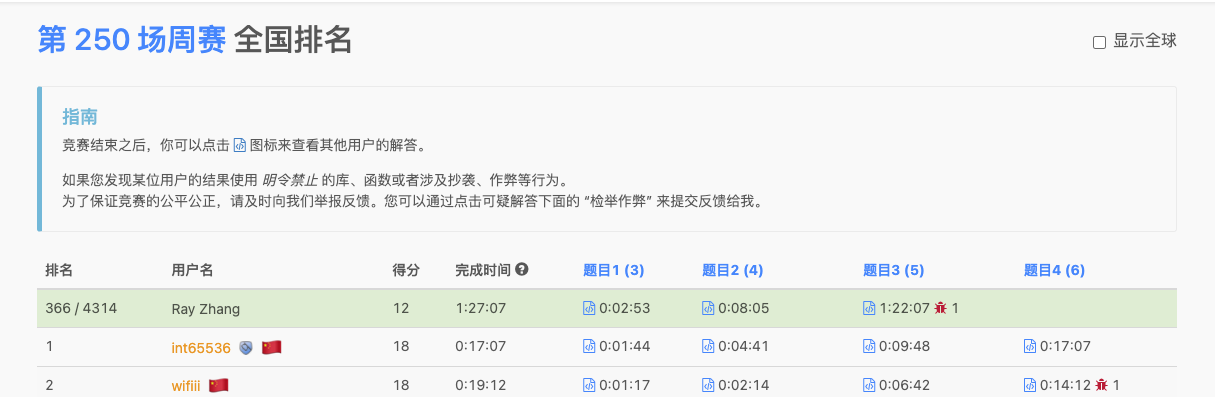
题目
键盘出现了一些故障,有些字母键无法正常工作。而键盘上所有其他键都能够正常工作。
给你一个由若干单词组成的字符串 text ,单词间由单个空格组成(不含前导和尾随空格);另有一个字符串 brokenLetters ,由所有已损坏的不同字母键组成,返回你可以使用此键盘完全输入的 text 中单词的数目。
示例 1:
输入:text = “hello world”, brokenLetters = “ad”
输出:1
解释:无法输入 “world” ,因为字母键 ‘d’ 已损坏。
示例 2:
输入:text = “leet code”, brokenLetters = “lt”
输出:1
解释:无法输入 “leet” ,因为字母键 ‘l’ 和 ‘t’ 已损坏。
示例 3:
输入:text = “leet code”, brokenLetters = “e”
输出:0
解释:无法输入任何单词,因为字母键 ‘e’ 已损坏。
提示:
1 <= text.length <= 10^4
0 <= brokenLetters.length <= 26
text 由若干用单个空格分隔的单词组成,且不含任何前导和尾随空格
每个单词仅由小写英文字母组成
brokenLetters 由 互不相同 的小写英文字母组成
题解
就是玩儿~爱咋写咋写
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public int canBeTypedWords(String text, String brokenLetters) {
String[] arr = text.split(" ");
int len = arr.length;
int res = 0;
for(int i = 0; i < len; i++){
int l = arr[i].length();
boolean flag = true;
for(int j = 0; j < l; j++){
if(brokenLetters.indexOf(arr[i].charAt(j)) != -1) {
flag = false;
break;
}
}
if(flag) res++;
}
return res;
}
}
|
题目
给你一个 严格递增 的整数数组 rungs ,用于表示梯子上每一台阶的 高度 。当前你正站在高度为 0 的地板上,并打算爬到最后一个台阶。
另给你一个整数 dist 。每次移动中,你可以到达下一个距离你当前位置(地板或台阶)不超过 dist 高度的台阶。当然,你也可以在任何正 整数 高度处插入尚不存在的新台阶。
返回爬到最后一阶时必须添加到梯子上的 最少 台阶数。
示例 1:
输入:rungs=[1,3,5,10],dist=2
输出:2
解释:
现在无法到达最后一阶。
在高度为 7 和 8 的位置增设新的台阶,以爬上梯子。
梯子在高度为 [1,3,5,7,8,10] 的位置上有台阶。
示例 2:
输入:rungs=[3,6,8,10],dist=3
输出:0
解释:
这个梯子无需增设新台阶也可以爬上去。
示例 3:
输入:rungs=[3,4,6,7],dist=2
输出:1
解释:
现在无法从地板到达梯子的第一阶。
在高度为 1 的位置增设新的台阶,以爬上梯子。
梯子在高度为 [1,3,4,6,7] 的位置上有台阶。
示例 4:
输入:rungs=[5],dist=10
输出:0
解释:这个梯子无需增设新台阶也可以爬上去。
提示:
1 <= rungs.length <= 10^5
1 <= rungs[i] <= 10^9
1 <= dist <= 10^9
rungs 严格递增
题解
贪心,由于数组是严格递增的,我们只需要将相邻元素的差取出和dist进行比较即可,对能否取整进行讨论即可,没什么难度
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int addRungs(int[] rungs, int dist) {
int len = rungs.length;
int res = 0;
for(int i = 0; i < len; i++){
int diff = rungs[i] - (i > 0 ? rungs[i - 1]: 0);
int tmp = diff / dist;
if(tmp * dist == diff) res += tmp - 1;
else res += tmp;
}
return res;
}
}
|
题目
给你一个 m x n 的整数矩阵 points (下标从 0 开始)。一开始你的得分为 0 ,你想最大化从矩阵中得到的分数。
你的得分方式为:每一行 中选取一个格子,选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。
然而,相邻行之间被选中的格子如果隔得太远,你会失去一些得分。对于相邻行 r 和 r + 1 (其中 0 <= r < m - 1),选中坐标为 (r, c1) 和 (r + 1, c2) 的格子,你的总得分 减少 abs(c1 - c2) 。
请你返回你能得到的 最大 得分。
abs(x) 定义为:
如果 x >= 0 ,那么值为 x 。
如果 x < 0 ,那么值为 -x 。
示例 1:
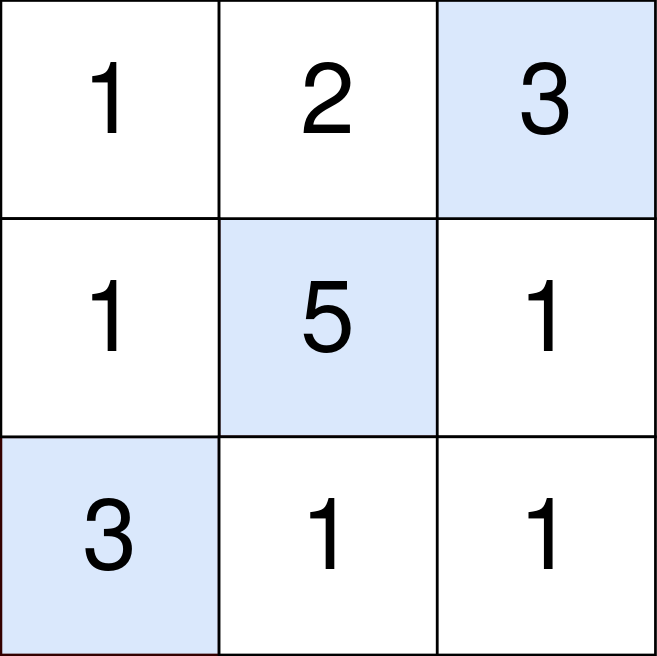
输入:points=[[1,2,3],[1,5,1],[3,1,1]]
输出:9
解释:
蓝色格子是最优方案选中的格子,坐标分别为 (0, 2),(1, 1) 和 (2, 0) 。
你的总得分增加 3 + 5 + 3 = 11 。
但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。
你的最终得分为 11 - 2 = 9 。
示例 2:
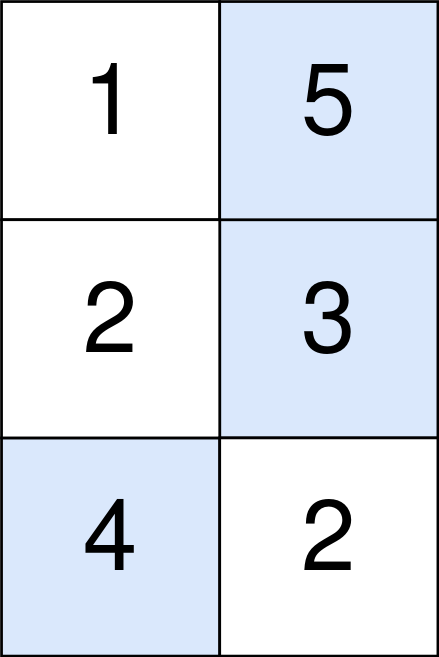
输入:points=[[1,5],[2,3],[4,2]]
输出:11
解释:
蓝色格子是最优方案选中的格子,坐标分别为 (0, 1),(1, 1) 和 (2, 0) 。
你的总得分增加 5 + 3 + 4 = 12 。
但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。
你的最终得分为 12 - 1 = 11 。
提示:
m==points.length
n==points[r].length
1<=m,n<=105
1<=m∗n<=105
0<=points[r][c]<=105
题解
又是险些翻大车的一天,t3做的脑子像是锈掉了,罚坐一个多小时才有了点想法
看到题目,首先想到DP动态规划,毕竟每一行的决策都是无后效性的,我们只需要研究后一行和前一行之间的关系即可,确保每一行各位置决策最优,则下一行决策也为最优
我们用dp[i][j]表示自上往下走到points[i][j]时刻的最优策略代表的分数
但是数据量我第一次看到时感到了些许迷惑,尤其是1<=m,n<=105,1<=m∗n<=105
数次尝试时我采用了简单暴力的DP,喜提了一发TLE,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
public long maxPoints(int[][] points) {
int rows = points.length;
int cols = points[0].length;
long[][] dp = new long[rows][cols];
for(int i = 0; i < cols; i++) dp[0][i] = points[0][i];
for(int i = 1; i < rows; i++){
for(int j = 0; j < cols; j++){
for(int k = 0; k < cols; k++){
dp[i][j] = Math.max(dp[i][j], dp[i - 1][k] + points[i][j] - Math.abs(j - k));
}
}
}
long res = 0;
for(int i = 0; i < cols; i++) res = Math.max(res, dp[rows - 1][i]);
return res;
}
}
|
易得复杂度为O(mn2),在m较小,n较大的情况下(如只有一二三四行,但是有数万列)会导致复杂度过高,说明算法有待优化
关键在于这段循环:
1
2
3
4
5
| for(int j = 0; j < cols; j++){
for(int k = 0; k < cols; k++){
dp[i][j] = Math.max(dp[i][j], dp[i - 1][k] + points[i][j] - Math.abs(j - k));
}
}
|
我在处理上行和下行的最优策略时 直接对新一行的各个元素 分别在上一行进行暴力遍历
即选中下行的位置,随后对上行所有可能的来源路径进行暴力枚举
导致发生了cols2次的计算,那么是否有办法优化这种暴力比较呢?
首先dp[i][j]的值由dp[i - 1][k] + points[i][j] - Math.abs(j - k)确定,但是points[i][j]是固定变量,因此解决本问题即解决dp[i - 1][k] - Math.abs(j - k)的最小值
此外我们发现处理绝对值的时候有个特点,如果两个上行元素a,b都在下行指定元素j的同一侧,如果有dp[i - 1][a] - Math.abs(j - a) < dp[i - 1][b] - Math.abs(j - b),那么随着j的不断移动,只要a,b维持在j的一侧,由于两者的相对距离固定,那么得分情况的相对大小也是必然确定的,最多在原来的基准上同加或者同减,该大的位置永远是大的(前提是在同一侧,不管是-Math.abs(j - k)递增的那一侧还是递减的那一侧)
那么我们就有思路喽:
我们定义一个left数组和right数组分别描述递增一侧和递减一侧情况,贯彻落实“同一侧大的永远是大的”这一简单思路
left[j]表示自最左端dp[i - 1][0]向右遍历到dp[i - 1][j]当前位置时刻,dp[i - 1][k] - Math.abs(j - k)产生的最大值,也就是j的左侧(包含j)产生的最大值,我们取j = 0作为left数组的基准,到时候具体计算dp[i][j]时只需要减去一个j变量即可(在原来的基准上同加或者同减)right[j]表示自最右端dp[i - 1][cols - 1]向左遍历到dp[i - 1][j]当前位置时刻,dp[i - 1][k] - Math.abs(j - k)产生的最大值,也就是j的右侧(包含j)产生的最大值,我们取j = cols - 1作为right数组的基准,到时候具体计算dp[i][j]时只需要加上一个j变量即可(在原来的基准上同加或者同减)
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
public long maxPoints(int[][] points) {
int rows = points.length;
int cols = points[0].length;
long[][] dp = new long[rows][cols];
for(int i = 0; i < cols; i++) dp[0][i] = points[0][i];
for(int i = 1; i < rows; i++){
long[] left = new long[cols];
long[] right = new long[cols];
left[0] = dp[i - 1][0];
right[cols - 1] = dp[i - 1][cols - 1] - cols + 1;
for(int j = 1; j < cols; j++){
left[j] = Math.max(left[j - 1], dp[i - 1][j] + j);
}
for(int j = cols - 2; j >= 0; j--){
right[j] = Math.max(right[j + 1], dp[i - 1][j] - j);
}
for(int j = 0; j < cols; j++){
dp[i][j] = Math.max(points[i][j] + left[j] - j, points[i][j] + right[j] + j);
}
}
long res = 0;
for(int i = 0; i < cols; i++) res = Math.max(res, dp[rows - 1][i]);
return res;
}
}
|
复杂度为O(mn),满足条件,可以正常通过
题目
给你一棵 n 个节点的有根树,节点编号从 0 到 n - 1 。每个节点的编号表示这个节点的 独一无二的基因值 (也就是说节点 x 的基因值为 x)。两个基因值的 基因差 是两者的 异或和 。给你整数数组 parents ,其中 parents[i] 是节点 i 的父节点。如果节点 x 是树的 根 ,那么 parents[x] == -1 。
给你查询数组 queries ,其中 queries[i] = [nodei, vali] 。对于查询 i ,请你找到 vali 和 pi 的 最大基因差 ,其中 pi 是节点 nodei 到根之间的任意节点(包含 nodei 和根节点)。更正式的,你想要最大化 vali XOR pi 。
请你返回数组 ans ,其中 ans[i] 是第 i 个查询的答案。
示例 1:

输入:parents=[−1,0,1,1],queries=[[0,2],[3,2],[2,5]]
输出:[2,3,7]
解释:查询数组处理如下:
[0,2]:最大基因差的对应节点为 0 ,基因差为 2 XOR 0 = 2 。
[3,2]:最大基因差的对应节点为 1 ,基因差为 2 XOR 1 = 3 。
[2,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
示例 2:

输入:parents=[3,7,−1,2,0,7,0,2],queries=[[4,6],[1,15],[0,5]]
输出:[6,14,7]
解释:查询数组处理如下:
[4,6]:最大基因差的对应节点为 0 ,基因差为 6 XOR 0 = 6 。
[1,15]:最大基因差的对应节点为 1 ,基因差为 15 XOR 1 = 14 。
[0,5]:最大基因差的对应节点为 2 ,基因差为 5 XOR 2 = 7 。
提示:
2<=parents.length<=105
对于每个 不是 根节点的 i ,有 0<=parents[i]<=parents.length−1 。
parents[root]==−1
1<=queries.length<=3∗104
0<=nodei<=parents.length−1
0<=vali<=2∗105
题解
本题是一道中规中矩的前缀树的题目,本题的简化模型可以简单参考leetcode 421. 数组中两个数的最大异或值,其中采用的数据结构和做法都是类似的,本题关键在于其离线算法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
| class Solution {
public int[] maxGeneticDifference(int[] parents, int[][] queries) {
Map<Integer, List<Integer>> tree = new HashMap<>();
for(int i = 0; i < parents.length; i++){
if(!tree.containsKey(parents[i])){
tree.put(parents[i], new ArrayList<>());
}
tree.get(parents[i]).add(i);
}
Map<Integer, Map<Integer, Integer>> queryMap = new HashMap<>();
for(int i = 0; i < queries.length; i++){
if(!queryMap.containsKey(queries[i][0])){
queryMap.put(queries[i][0], new HashMap<Integer, Integer>());
}
queryMap.get(queries[i][0]).put(queries[i][1], 0);
}
dfs(new ZeroOneTrie(), tree, queryMap, tree.get(-1).get(0));
int[] r = new int[queries.length];
for(int i = 0;i < r.length; i++){
r[i] = queryMap.get(queries[i][0]).get(queries[i][1]);
}
return r;
}
private void dfs(ZeroOneTrie zeroOneTrie, Map<Integer, List<Integer>> tree,
Map<Integer, Map<Integer, Integer>> queryMap, int root) {
zeroOneTrie.insert(root);
if(queryMap.containsKey(root)){
Map<Integer, Integer> resMap = queryMap.get(root);
for (Integer query : resMap.keySet()) {
resMap.put(query,query ^ zeroOneTrie.queryMax(query));
}
}
if(tree.containsKey(root)){
List<Integer> next = tree.get(root);
for(int r : next){
dfs(zeroOneTrie,tree,queryMap,r);
}
}
zeroOneTrie.delete(root);
}
public class ZeroOneTrie{
private class Node{
public int count = 0;
public int val = 0;
public Node[] next = new Node[2];
}
Node root = new Node();
public void insert(int num){
Node cur = root;
for(int i = 31; i >= 0; i--){
int op = ((num >> i) & 1);
if(cur.next[op] == null){
cur.next[op] = new Node();
}
cur = cur.next[op];
cur.count++;
}
cur.val = num;
}
public void delete(int num){
Node cur = root;
for(int i = 31; i >= 0; i--){
int op = ((num >> i) & 1);
if(cur.next[op].count == 1){
cur.next[op] = null;
return;
}
else{
cur = cur.next[op];
cur.count--;
}
}
}
public int queryMax(int num){
Node cur = root;
for(int i = 31; i >= 0; i--){
int op = ((num >> i) & 1) == 0 ? 1 : 0;
if(cur.next[op] != null){
cur = cur.next[op];
}
else{
op = op ^ 1;
cur=cur.next[op];
}
}
return cur.val;
}
public int queryMin(int num){
Node cur = root;
for(int i = 31; i >= 0; i--){
int op = ((num >> i) & 1);
if(cur.next[op] != null){
cur = cur.next[op];
}
else{
cur = cur.next[op ^ 1];
}
}
return cur.val;
}
}
}
|
















