T1 5804. 检查是否所有字符出现次数相同

题目

给你一个字符串 s ，如果 s 是一个 好 字符串，请你返回 true ，否则请返回 false 。
如果 s 中出现过的 所有 字符的出现次数 相同 ，那么我们称字符串 s 是 好 字符串。

示例 1：
输入：s = “abacbc”
输出：true
解释：s 中出现过的字符为 ‘a’，‘b’ 和 ‘c’ 。s 中所有字符均出现 2 次。

示例 2：
输入：s = “aaabb”
输出：false
解释：s 中出现过的字符为 ‘a’ 和 ‘b’ 。
‘a’ 出现了 3 次，‘b’ 出现了 2 次，两者出现次数不同。
 
提示：
1 <= s.length <= 1000
s 只包含小写英文字母。

题解

随意了，反正是要前后比较的，prev的临时参数少不了，map数组都一样

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public boolean areOccurrencesEqual(String s) {
        Map<Character, Integer> map = new HashMap<>();
        int len = s.length();
        for(int i = 0; i < len; i++){
            char ch = s.charAt(i);
            map.put(ch, map.getOrDefault(ch, 0) + 1);
        }
        int prev = -1;
        for(char x: map.keySet()){
            if(prev == -1){
                prev = map.get(x);
                continue;
            }
            if(map.get(x) != prev) return false;
            prev = map.get(x);
        }
        return true;
    }
}

T2 5805. 最小未被占据椅子的编号

题目

有 n 个朋友在举办一个派对，这些朋友从 0 到 n - 1 编号。派对里有 无数 张椅子，编号为 0 到 infinity 。当一个朋友到达派对时，他会占据 编号最小 且未被占据的椅子。
比方说，当一个朋友到达时，如果椅子 0 ，1 和 5 被占据了，那么他会占据 2 号椅子。
当一个朋友离开派对时，他的椅子会立刻变成未占据状态。如果同一时刻有另一个朋友到达，可以立即占据这张椅子。
给你一个下标从 0 开始的二维整数数组 times ，其中 times[i] = [arrivali, leavingi] 表示第 i 个朋友到达和离开的时刻，同时给你一个整数 targetFriend 。所有到达时间 互不相同 。
请你返回编号为 targetFriend 的朋友占据的 椅子编号 。

示例 1：
输入：times = [[1,4],[2,3],[4,6]], targetFriend = 1
输出：1
解释：
朋友 0 时刻 1 到达，占据椅子 0 。
朋友 1 时刻 2 到达，占据椅子 1 。
朋友 1 时刻 3 离开，椅子 1 变成未占据。
朋友 0 时刻 4 离开，椅子 0 变成未占据。
朋友 2 时刻 4 到达，占据椅子 0 。
朋友 1 占据椅子 1 ，所以返回 1 。

示例 2：
输入：times = [[3,10],[1,5],[2,6]], targetFriend = 0
输出：2
解释：
朋友 1 时刻 1 到达，占据椅子 0 。
朋友 2 时刻 2 到达，占据椅子 1 。
朋友 0 时刻 3 到达，占据椅子 2 。
朋友 1 时刻 5 离开，椅子 0 变成未占据。
朋友 2 时刻 6 离开，椅子 1 变成未占据。
朋友 0 时刻 10 离开，椅子 2 变成未占据。
朋友 0 占据椅子 2 ，所以返回 2 。
 
提示：
n == times.length
2 <= n <= 10^4
times[i].length == 2
1 <= arrivali < leavingi <= 10^5
0 <= targetFriend <= n - 1
每个 arrivali 时刻 互不相同 。

题解

暴力模拟就好了，貌似还有更优解，下次看看

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int smallestChair(int[][] times, int targetFriend) {
        int len = times.length;
        Integer[] arr = new Integer[len];
        for(int i = 0; i < len; i++) arr[i] = i;
        Arrays.sort(arr, (o1, o2) -> times[o1][0] - times[o2][0]);
        Set<Integer> set = new HashSet<>();
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[0] - o2[0]);
        for(int i = 0; i < len; i++){
            while(!pq.isEmpty() && pq.peek()[0] <= times[arr[i]][0]){
                int[] cur = pq.poll();
                set.remove(cur[1]);
            }
            for(int k = 0; k <= Integer.MAX_VALUE; k++){
                if(!set.contains(k)){
                    set.add(k);
                    pq.offer(new int[]{times[arr[i]][1], k});
                    if(arr[i] == targetFriend) return k;
                    break;
                }
            }
        }
        return -1;
    }
}

T3 5806. 描述绘画结果

题目

给你一个细长的画，用数轴表示。这幅画由若干有重叠的线段表示，每个线段有 独一无二 的颜色。给你二维整数数组 segments ，其中 segments[i] = [starti, endi, colori] 表示线段为 半开区间 [starti, endi) 且颜色为 colori 。
线段间重叠部分的颜色会被 混合 。如果有两种或者更多颜色混合时，它们会形成一种新的颜色，用一个 集合 表示这个混合颜色。
比方说，如果颜色 2 ，4 和 6 被混合，那么结果颜色为 {2,4,6} 。
为了简化题目，你不需要输出整个集合，只需要用集合中所有元素的 和 来表示颜色集合。
你想要用 最少数目 不重叠 半开区间 来 表示 这幅混合颜色的画。这些线段可以用二维数组 painting 表示，其中 painting[j] = [leftj, rightj, mixj] 表示一个 半开区间[leftj, rightj) 的颜色 和 为 mixj 。

  • 比方说，这幅画由 segments = [[1,4,5],[1,7,7]] 组成，那么它可以表示为 painting = [[1,4,12],[4,7,7]] ，因为：
    • [1,4) 由颜色 {5,7} 组成（和为 12），分别来自第一个线段和第二个线段。
    • [4,7) 由颜色 {7} 组成，来自第二个线段。
      请你返回二维数组 painting ，它表示最终绘画的结果（没有 被涂色的部分不出现在结果中）。你可以按 任意顺序 返回最终数组的结果。
      半开区间 [a, b) 是数轴上点 a 和点 b 之间的部分，包含 点 a 且 不包含 点 b 。

示例 1：

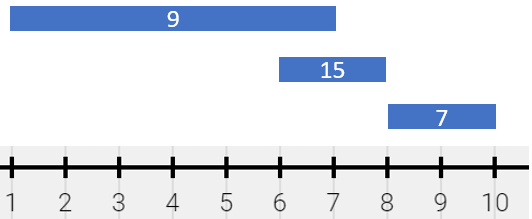
输入：segments = [[1,4,5],[4,7,7],[1,7,9]]
输出：[[1,4,14],[4,7,16]]
解释：绘画借故偶可以表示为：
[1,4) 颜色为 {5,9} （和为 14），分别来自第一和第二个线段。
[4,7) 颜色为 {7,9} （和为 16），分别来自第二和第三个线段。

示例 2：

输入：segments = [[1,7,9],[6,8,15],[8,10,7]]
输出：[[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
解释：绘画结果可以以表示为：
[1,6) 颜色为 9 ，来自第一个线段。
[6,7) 颜色为 {9,15} （和为 24），来自第一和第二个线段。
[7,8) 颜色为 15 ，来自第二个线段。
[8,10) 颜色为 7 ，来自第三个线段。

示例 3：

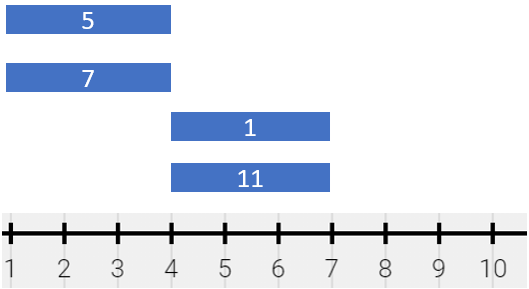
输入：segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
输出：[[1,4,12],[4,7,12]]
解释：绘画结果可以表示为：
[1,4) 颜色为 {5,7} （和为 12），分别来自第一和第二个线段。
[4,7) 颜色为 {1,11} （和为 12），分别来自第三和第四个线段。
注意，只返回一个单独的线段 [1,7) 是不正确的，因为混合颜色的集合不相同。

提示：
1 <= segments.length <= 2 * 10^4
segments[i].length == 3
1 <= starti < endi <= 10^5
1 <= colori <= 10^9
每种颜色 colori 互不相同。

题解

看到题目顺畅的想到差分，再看看数据区间范围
emmmm，其实开数组和开TreeMap应该都可，私以为TreeMap可能是更优解
虽然在时间复杂度可能上不如数组来的快，但是Map中的每一个key分别代表了各个区间的两个端点，这样子在相邻两段 和相同但是组成不一致 的时候就可以直接区分出来，非常的方便
代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
    public List<List<Long>> splitPainting(int[][] segments) {
        TreeMap<Long, Long> map = new TreeMap<>();
        int len = segments.length;
        for(int[] x: segments){
            map.put(x[0] * 1L, map.getOrDefault(x[0] * 1L, 0L) + x[2] * 1L);
            map.put(x[1] * 1L, map.getOrDefault(x[1] * 1L, 0L) - x[2] * 1L);
        }
        long cur = 0;
        Long prev = null;
        List<List<Long>> res = new ArrayList<>();
        for(long x: map.keySet()){
            if(prev != null && cur != 0){
                List<Long> list = new ArrayList<>();
                list.add(prev);
                list.add(x);
                list.add(cur);
                res.add(list);
            }
            cur += map.get(x);
            if(prev == null){
                prev = x;
                continue;
            }
            prev = x;
        }
        return res;
    }
}

T4 5196. 队列中可以看到的人数

题目

有 n 个人排成一个队列，从左到右 编号为 0 到 n - 1 。给你以一个整数数组 heights ，每个整数 互不相同，heights[i] 表示第 i 个人的高度。
一个人能 看到 他右边另一个人的条件是这两人之间的所有人都比他们两人 矮 。更正式的，第 i 个人能看到第 j 个人的条件是 i < j 且 min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1]) 。
请你返回一个长度为 n 的数组 answer ，其中 answer[i] 是第 i 个人在他右侧队列中能 看到 的 人数 。

示例 1：

输入：heights = [10,6,8,5,11,9]
输出：[3,1,2,1,1,0]
解释：
第 0 个人能看到编号为 1 ，2 和 4 的人。
第 1 个人能看到编号为 2 的人。
第 2 个人能看到编号为 3 和 4 的人。
第 3 个人能看到编号为 4 的人。
第 4 个人能看到编号为 5 的人。
第 5 个人谁也看不到因为他右边没人。

示例 2：
输入：heights = [5,1,2,3,10]
输出：[4,1,1,1,0]

提示：
n == heights.length
1 <= n <= 10^5
1 <= heights[i] <= 10^5
heights 中所有数 互不相同 。

题解

就是简单的单调栈，但是如果出栈结束后栈非空的话要特判一下，人傻了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    
    public int[] canSeePersonsCount(int[] heights) {
        Stack<Integer> st = new Stack<>();
        int len = heights.length;
        int[] res = new int[len];
        for(int i = len - 1; i >= 0; i--){
            while(!st.isEmpty() && heights[st.peek()] < heights[i]){
                st.pop();
                res[i]++;
            }
            if(!st.isEmpty()) res[i]++;
            st.push(i);
        }
        return res;
    }
}