最短路问题 | Ray's Blog

简介

最短路径问题是图论研究中的一个经典算法问题，旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。

算法具体的形式包括：

确定起点的最短路径问题 - 也叫单源最短路问题，即已知起始结点，求最短路径的问题。在边权非负时适合使用Dijkstra算法，若边权为负时则适合使用Bellman-ford算法或者SPFA算法。
确定终点的最短路径问题 - 与确定起点的问题相反，该问题是已知终结结点，求最短路径的问题。在无向图中该问题与确定起点的问题完全等同，在有向图中该问题等同于把所有路径方向反转的确定起点的问题。
确定起点终点的最短路径问题 - 即已知起点和终点，求两结点之间的最短路径。
全局最短路径问题 - 也叫多源最短路问题，求图中所有的最短路径。适合使用Floyd-Warshall算法。

有向图的表示

首先最短路径问题面向的是有向图，而无向图的话显然我可以认为是一种特殊的有向图，即每条边都是双向的。

假设给定1, 2, 3, ..., n共n个节点，那么我们可以如何描述点与点之间的关系呢？

例如下图：

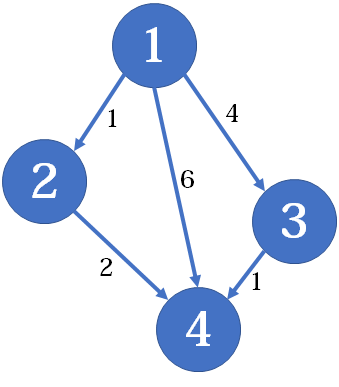
edges数组表示

首先我们可以单纯的根据边的情况来进行描述，可以表示为：

1	int[][] edges = {{1, 2, 1}, {1, 4, 6}, {1, 3, 4}, {2, 4, 2}, {3, 4, 1}};

其中对于第i个元素，我们将其描述为一条有向边，一个edge数组包含了[from, to, cost]三个部分，from表示边的起始节点编号，to表示边的目的地节点编号，cost表示途径这条边所花费的代价。

虽然我们把当前有向图的相关信息都表示出来了，但是缺点也是显而易见的，我们无法单纯的通过一条边来确定节点的相关信息，甚至连节点的邻接节点相关信息都不能有效的提取，这样的表示形式需要适当的转化。

邻接矩阵表示

我们维护一张如下的 $n \times n$ 矩阵表

cost	1(to)	2(to)	3(to)	4(to)
1(from)	0	1	4	6
2(from)	INF	0	INF	2
3(from)	INF	INF	0	1
4(from)	INF	INF	INF	0

其中cost[i][j]表示的是从i连接到j的距离，这种矩阵表示就显得简单易懂了，很显然的节点自身和节点自身的距离必然为0，当边不存在时我们认为两点之间的距离为无穷大也就是我们表中所标志的INF。

当然这种表格不仅可以用于表示初始状态相关信息，我们在某些算法中可以直接对邻接矩阵进行实时更新，最终将点与点之间到最短距离关系直接体现在矩阵中。

在代码中，我们可以这么表示矩阵间的关系，由于，节点下标从1开始取，为了方便我们也可以建立 $n + 1 \times n + 1$ 矩阵，将cost[0][i]与cost[i][0]部分使用INF进行填充，即认为存在0号节点但是与其他节点没有任何交集，或者我们将下标直接缩减一也可。总之找到正确的对应关系即可。

public static final int INF = Integer.MAX_VALUE / 2;
int[][] matrix = {
  {0, INF, INF, INF, INF}, 
  {INF, 0, 1, 4, 6}, 
  {INF, INF, 0, INF, 2}, 
  {INF, INF, INF, 0, 1}, 
  {INF, INF, INF, INF, 0}
};

将edges数组转化为matrix矩阵，可以使用如下代码：

int n = 4;
public static final int INF = Integer.MAX_VALUE / 2;
int[][] edges = {{1, 2, 1}, {1, 4, 6}, {1, 3, 4}, {2, 4, 2}, {3, 4, 1}};
int[][] matrix = new int[n + 1][n + 1];
for(int[] x: matrix) Arrays.fill(x, INF);
for(int i = 0; i <= n; i++) matrix[i][i] = 0;
for(int[] edge: edges){
  matrix[edge[0]][edge[1]] = edge[2];
}

使用`List<List<int[]>>`进行有限填充

上面的matrix数组很直观的表示了点与点之间的关系，但是也存储了大量的无关信息，例如自身和自身距离为0，不接触节点距离为INF等信息，将数据量扩容到 $n \times n$ 水平。所以我们可以考虑使用List<List<Integer>>来存储每个点的邻接相关信息。

例如节点1，邻接节点分别有2, 3, 4三个节点，权重分别为1, 6, 4。我们就可以向neighbour.get(1)中加入{2, 1},{3, 6},{4, 4}三个小数组，表示1号节点的邻接节点和权重相关信息。

Index	Edges
0
1	{2, 1}, {3, 6}, {4, 4}
2	{4, 2}
3	{4, 1}
4

我们将edge数组转化为List<List<Integer>>也可以通过如下方法来实现：

int n = 4;
int[][] edges = {{1, 2, 1}, {1, 4, 6}, {1, 3, 4}, {2, 4, 2}, {3, 4, 1}};
List<List<int[]>> neighbour = new ArrayList<>();
for(int i = 0; i <= n; i++){
  neighbour.add(new ArrayList<int[]>());
}
for(int[] edge: edges){
  neighbour.get(edge[0]).add(new int[]{edge[1], edge[2]});
}

Dijkstra迪杰斯特拉算法

迪杰斯特拉(Dijkstra)算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。
它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止。

基本思想

通过Dijkstra计算图G中的最短路径时，需要指定起点s(即从顶点s开始计算)。

此外，引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度)，而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。

初始时，S中只有起点s；U中是除s之外的顶点，并且U中顶点的路径是"起点s到该顶点的路径"。然后，从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。然后，再从U中找出路径最短的顶点，并将其加入到S中；接着，更新U中的顶点和顶点对应的路径。 … 重复该操作，直到遍历完所有顶点。

一点小小的个人思考，感觉有点类似贪心，即认为“已经确认的最短节点延伸出来的各个节点中最短者必然是正确解”，我们将正确解纳入已经确认的最短节点中，并对其继续扩展

操作步骤

初始时，S只包含起点s；U包含除s外的其他顶点，且U中顶点的距离为"起点s到该顶点的距离"

例如，U中顶点v的距离为(s,v)的长度，然后s和v不相邻，则v的距离为∞。
从U中选出"距离最短的顶点k"，并将顶点k加入到S中；同时，从U中移除顶点k。
更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其它顶点的距离；例如，(s,v)的距离可能大于(s,k)+(k,v)的距离。
重复步骤(2)和(3)，直到遍历完所有顶点。

举例

以第4个顶点D为起点

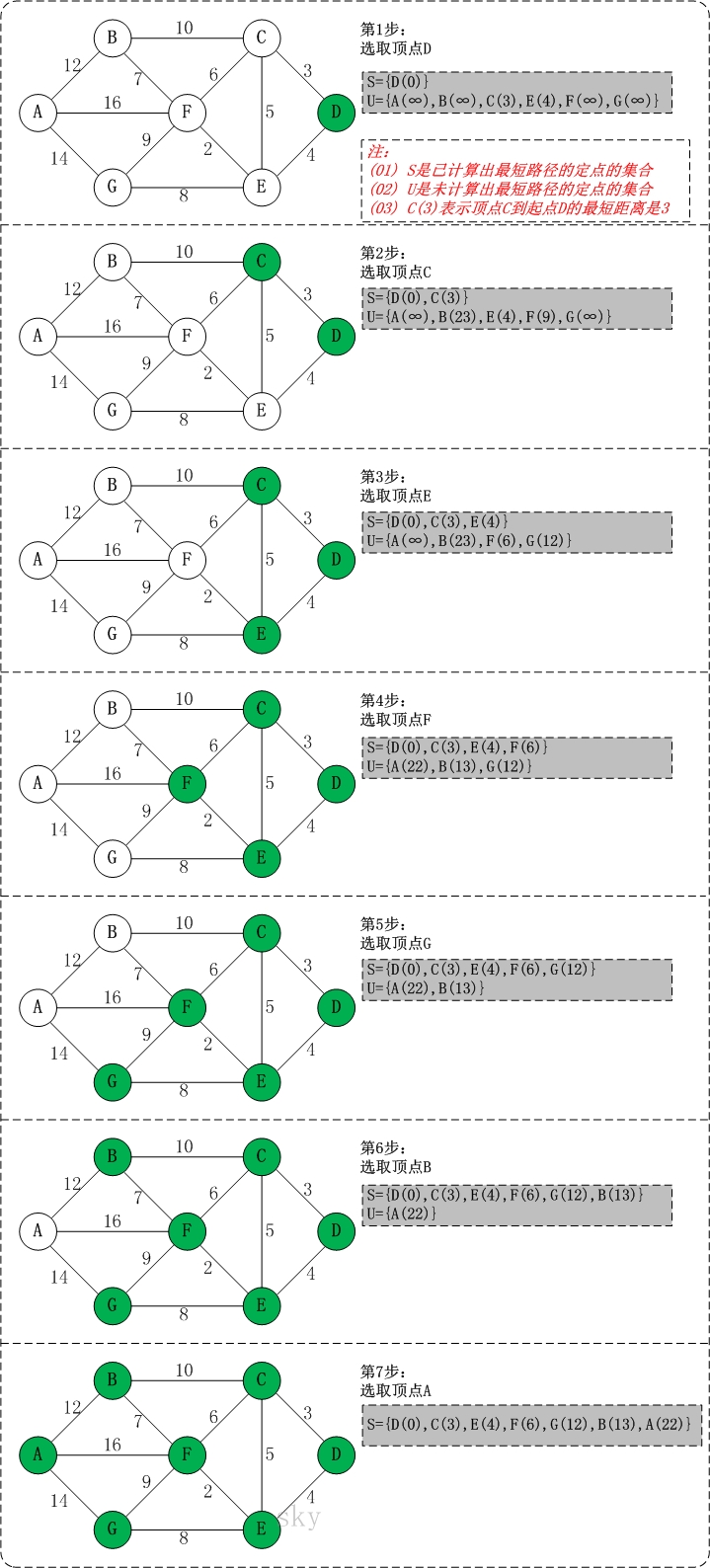
实现逻辑

如果我们采用matrix矩阵进行相关操作，注意到Dijkstra复杂度为 $O(n^2)$

那么：

public class Test {
    public static void main(String[] args) {
        int MAX = Integer.MAX_VALUE;    // 无法到达时距离设为 Integer.MAX_VALUE
        int[][] weight={
                {0,1,12,MAX,MAX,MAX},
                {MAX,0,9,3,MAX,MAX},
                {MAX,MAX,0,MAX,5,MAX},
                {MAX,MAX,4,0,13,15},
                {MAX,MAX,MAX,MAX,0,4},
                {MAX,MAX,MAX,MAX,MAX,0}
        };
        int start = 0;  // 选择出发点
        System.out.println(Arrays.toString(solution(weight,start)));
    }

    private static int[] solution(int[][] weight, int start) {
        boolean[] visit = new boolean[weight.length]; // 标记某节点是否被访问过
        int[] res = new int[weight.length];     // 记录 start 点到各点的最短路径长度
        for (int i = 0; i < res.length; i++) {
            res[i] = weight[start][i];
        }

        // 查找 n - 1 次（n 为节点个数），每次确定一个节点
        for(int i = 1; i < weight.length; i++) {
            int min = Integer.MAX_VALUE;
            int p = 0;
            // 找出一个未标记的离出发点最近的节点
            for(int j = 0; j < weight.length; j++){
                if(j != start && !visit[j] && res[j] < min){
                    min = res[j];
                    p = j;
                }
            }
            // 标记该节点为已经访问过
            visit[p] = true;

            for (int j = 0; j < weight.length; j++){
                if (j == p || weight[p][j] == Integer.MAX_VALUE) {  // p 点不能到达 j
                    continue;
                }
                if (res[p] + weight[p][j] < res[j]){
                    res[j] = res[p] + weight[p][j];  //更新最短路径
                }
            }
        }

        return res;
    }
}

如果采用List<List<Integer>>那么效果也是类似的，每次拓展出来从优先队列中拿出长度最小的节点，进行比较和修改。

class Solution {
    public int[] getDistance(int n, int[][] edges) {
        int[] distance = new int[n + 1];
        Arrays.fill(distance, Integer.MAX_VALUE);
        boolean[] visited = new boolean[n + 1];
        List<List<int[]>> adjacency = new ArrayList<>();
        for(int i = 0; i <= n; i++){
            adjacency.add(new ArrayList<int[]>());
        }
        for(int[] edge: edges){
            adjacency.get(edge[0]).add(new int[]{edge[1], edge[2]});
        }
        distance[n] = 0;
        PriorityQueue<Integer> pq = new PriorityQueue<>((o1, o2) -> distance[o1] - distance[o2]);
        pq.offer(n);
        while(!pq.isEmpty()){
            int cur = pq.poll();
            if(visited[cur]) continue;
            visited[cur] = true;
            for(int[] x: adjacency.get(cur)){
                if(!visited[x[0]]){
                    distance[x[0]] = Math.min(distance[x[0]], distance[cur] + x[1]);
                    pq.offer(x[0]);
                }
            }
        }
      	return distance;
    }
}

Floyd算法

我们用Floyd算法解决多源最短路问题

通过Floyd算法，我们可以获得当前图中每个点两两之间的最短距离关系

Floyd本质上是一个动态规划的思想，每一次循环更新经过前k个节点，i到j的最短路径。

例如如图：

第一趟，k=1：

很明显，没有一个距离能通过经由1号点而减短。

第二趟，k=2：

这里，dist[1][4]通过经由2号点，最短路径缩短了。

第三趟，k=3：

这时虽然1->3->4的路径比1->4短，但是dist[1][4]已经被更新为3了，所以这一趟又白跑了。接下来k=4显然也更新不了任何点。综上，每一趟二重循环，实际上都是在考察，能不能经由k点，把i到j的距离缩短

Floyd的时间复杂度显然是 $O(n^3)$ ，同时拥有 $O(n^2)$ 的空间复杂度，都比较高，所以只适用于数据规模较小的情形。

基本思想

通过Floyd计算图G=(V,E)中各个顶点的最短路径时，需要引入一个矩阵S，矩阵S中的元素a[i][j]表示顶点i(第i个顶点)到顶点j(第j个顶点)的距离。

假设图G中顶点个数为N，则需要对矩阵S进行N次更新。初始时，矩阵S中顶点a[i][j]的距离为顶点i到顶点j的权值；如果i和j不相邻，则a[i][j] = ∞。接下来开始，对矩阵S进行N次更新。第1次更新时，如果a[i][j]的距离" > “a[i][0]+a[0][j](a[i][0]+a[0][j]表示"i与j之间经过第1个顶点的距离”)，则更新a[i][j]为"a[i][0]+a[0][j]“。同理，第k次更新时，如果"a[i][j]的距离” > “a[i][k]+a[k][j]”，则更新a[i][j]为"a[i][k]+a[k][j]"。更新N次之后，操作完成！

实现逻辑

public void floyd(int[][] path, int[][] dist) {

    // 初始化
    for (int i = 0; i < mVexs.length; i++) {
        for (int j = 0; j < mVexs.length; j++) {
            dist[i][j] = mMatrix[i][j];    // "顶点i"到"顶点j"的路径长度为"i到j的权值"。
            path[i][j] = j;                // "顶点i"到"顶点j"的最短路径是经过顶点j。
        }
    }

    // 计算最短路径
    for (int k = 0; k < mVexs.length; k++) {
        for (int i = 0; i < mVexs.length; i++) {
            for (int j = 0; j < mVexs.length; j++) {

                // 如果经过下标为k顶点路径比原两点间路径更短，则更新dist[i][j]和path[i][j]
                int tmp = (dist[i][k]==INF || dist[k][j]==INF) ? INF : (dist[i][k] + dist[k][j]);
                if (dist[i][j] > tmp) {
                    // "i到j最短路径"对应的值设，为更小的一个(即经过k)
                    dist[i][j] = tmp;
                    // "i到j最短路径"对应的路径，经过k
                    path[i][j] = path[i][k];
                }
            }
        }
    }

    // 打印floyd最短路径的结果
    System.out.printf("floyd: \n");
    for (int i = 0; i < mVexs.length; i++) {
        for (int j = 0; j < mVexs.length; j++)
            System.out.printf("%2d  ", dist[i][j]);
        System.out.printf("\n");
    }
}