都大四了就不能安分点,选个正常的选修课不好么🤦♂️
选错了课,一边上课一边备战秋招补录,上课上了个寂寞,等秋招基本结束了,大作业来了🤦♂️
关于数字图像处理,我的表情是这样的🤷♂️还得拿起万年不用的C++
开始
题目要求
采用已学习的图像二值化、团块分析、几何校正等算法,对所给的一组具有透视畸变的文本图像进行处理,要求将图像纠成正视图。
例如:
更多的测试样例如:
[{"url":"t1.jpg","alt":""},{"url":"t2.jpg","alt":""},{"url":"t3.jpg","alt":""},{"url":"t4.jpg","alt":""},{"url":"t5.jpg","alt":""},{"url":"t6.jpg","alt":""},{"url":"t7.jpg","alt":""},{"url":"t8.jpg","alt":""},{"url":"t9.jpg","alt":""},{"url":"t10.jpg","alt":""},{"url":"t11.jpg","alt":""}]
Load More
初步思路
我头几天的时间都在漫无目的地搜罗信息,我觉得还是这篇写得比较好(
文本图像的几何畸变校正技术研究
大致根据这篇文章的理解,我自己脑补出了如下的步骤:
进行噪声的消除,避免对后续处理的一些影响
将彩色图像转化为灰度图
进行二值化算法处理,把文字部分凸显出来,将背景和一些不相关的细节进行扣除
使用膨胀和腐蚀算法,在去除一些无效的字迹污点的同时,将文字进行横向水平的涂抹膨胀,将整行连成一片。各行生成独立的联通域。
联通域进行边缘检测提取,将顶部、底部、左部、右部的特征点分割出来。
对四条边上的特征点进行最小二乘法直线拟合,获得四条边,四条边求交点获得外接四边形的四角左边。
套用透视变换的公式,反结出变换的3 × 3 3 \times 3 3 × 3
鉴于我垃圾的C++代码能力,我的作业可以说就是超级缝合怪(能跑就行了属于是)
简介
问题引入
在使用扫描仪或者数码相机时,由于文本表面倾斜、弯曲或者一些其他人为的操作产生的拍摄视角的倾斜等原因,使得所拍摄到的文本图像存在比较严重的几何畸变。
这些畸变对文字处理 OCR 识别等工作都会带来极大的困难。因此必须要对变形的文本进行矫正,本作业以常见的由于拍摄角度导致的透视畸变为例,尝试对发生畸变的文本图像进行处理。
透视畸变介绍
透视变形有两种形式:扩展变形和压缩变形,在讨论同一成像面积上的图像时也被称作广角失真和长焦失真。
扩展变形可以看作是用广角镜头近拍得到的图像。离镜头近的物体与远处物体相比显得比正常尺寸大,而远处物体显得比正常尺寸小而且远——所以距离被扩展了。压缩变形可以看作是用长焦镜头在远处拍摄到的图像。物体无论远近看起来大小大致相同——较近的物体显得比正常尺寸小,而较远的物体显得比正常尺寸大,这样便无法区分远近物体的距离——所以距离被压缩了。
透视变形是由距离引起的,而非镜头,即在同一距离拍摄同一场景,无论用什么镜头,拍到的透视变形都是完全相同的。
对于文本图像的透视畸变而言的话,如果文本表面并无一些严重的弯曲现象,即正视图是横平竖直的排布的话,畸变后的图像应该也遵循相应的对齐特性,文字行与行,列与列之间,应该也满足对应的共线关系。
灰度图转化
对正常的彩色图片来说,每个像素点内部都包含了三个通道,分别代表了R , G , B R,G,B R , G , B
为了区分文字和背景,我们需要二值化算法来实现,为了简便相关的操作,我们选择将图像转换为灰度图像。
灰度化在图像处理中很常见,我们在生产应用中普遍使用公式:
G r a y = R ∗ 0.299 + G ∗ 0.597 + B ∗ 0.114 Gray = R * 0.299 + G * 0.597 + B * 0.114 G r a y = R ∗ 0.299 + G ∗ 0.597 + B ∗ 0.114
分别对红绿蓝三个分量的亮度值进行加权处理。 从公式中也可以看到,绿色相对于其他颜色会更加亮一些,红色次之,蓝色最弱。
在 OpenCV 中,我们也集成自带的方法,可以直接使用 cvtColor 方法,直接实现彩色图到灰度图到转换。
简单的实现代码如下:
1 2 3 4 5 6 7 using namespace cv;Mat toGray (Mat& src) { Mat srcGray; cvtColor (src, srcGray, COLOR_RGB2GRAY); return srcGray; }
图像去噪
空域法去噪
图片中可能会存在着大量的椒盐噪声,这些噪声的存在对后续二值化的处理可能会造成很大的困扰,算法可能无法将具体的文字和噪声颗粒进行区分。在空域上,比较典型的算法有邻域平均法。
邻域平均法,原理即为遍历图中的各个像素点,以当前的像素点为中心,取出各个像素点的邻域像素点窗口集合,邻域的选取标准可以有多种,例如选取4-邻域或者8-邻域,也可以选择更大的n × n n \times n n × n
公式表示记为:
G ( i , j ) = 1 L ∑ ( x , y ) ∈ A F ( x , y ) G(i,j)=\frac{1}{L}\sum\limits_{(x,y)\in A}{F(x,y)} G ( i , j ) = L 1 ( x , y ) ∈ A ∑ F ( x , y )
其中G ( i , j ) G(i,j) G ( i , j ) F ( i , j ) F(i,j) F ( i , j ) A A A L L L
简单的代码实现如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 Mat AverFiltering (Mat &src) { Mat dst (src.size(), src.type()) ; if (!src.data) return dst; for (int i = 1 ; i < src.rows; ++i) { for (int j = 1 ; j < src.cols; ++j) { if ((i - 1 >= 0 ) && (j - 1 ) >= 0 && (i + 1 ) < src.rows && (j + 1 ) < src.cols) { dst.at <Vec3b>(i, j)[0 ] = (src.at <Vec3b>(i, j)[0 ] + src.at <Vec3b>(i - 1 , j - 1 )[0 ] + src.at <Vec3b>(i - 1 , j)[0 ] + src.at <Vec3b>(i, j - 1 )[0 ] + src.at <Vec3b>(i - 1 , j + 1 )[0 ] + src.at <Vec3b>(i + 1 , j - 1 )[0 ] + src.at <Vec3b>(i + 1 , j + 1 )[0 ] + src.at <Vec3b>(i, j + 1 )[0 ] + src.at <Vec3b>(i + 1 , j)[0 ]) / 9 ; dst.at <Vec3b>(i, j)[1 ] = (src.at <Vec3b>(i, j)[1 ] + src.at <Vec3b>(i - 1 , j - 1 )[1 ] + src.at <Vec3b>(i - 1 , j)[1 ] + src.at <Vec3b>(i, j - 1 )[1 ] + src.at <Vec3b>(i - 1 , j + 1 )[1 ] + src.at <Vec3b>(i + 1 , j - 1 )[1 ] + src.at <Vec3b>(i + 1 , j + 1 )[1 ] + src.at <Vec3b>(i, j + 1 )[1 ] + src.at <Vec3b>(i + 1 , j)[1 ]) / 9 ; dst.at <Vec3b>(i, j)[2 ] = (src.at <Vec3b>(i, j)[2 ] + src.at <Vec3b>(i - 1 , j - 1 )[2 ] + src.at <Vec3b>(i - 1 , j)[2 ] + src.at <Vec3b>(i, j - 1 )[2 ] + src.at <Vec3b>(i - 1 , j + 1 )[2 ] + src.at <Vec3b>(i + 1 , j - 1 )[2 ] + src.at <Vec3b>(i + 1 , j + 1 )[2 ] + src.at <Vec3b>(i, j + 1 )[2 ] + src.at <Vec3b>(i + 1 , j)[2 ]) / 9 ; } else { dst.at <Vec3b>(i, j)[0 ] = src.at <Vec3b>(i, j)[0 ]; dst.at <Vec3b>(i, j)[1 ] = src.at <Vec3b>(i, j)[1 ]; dst.at <Vec3b>(i, j)[2 ] = src.at <Vec3b>(i, j)[2 ]; } } } return dst; }
值得注意的是当我们使用邻域平均法对图像进行平滑处理时,邻域平均法的平均作用会引起模糊现象,并且模糊程度与所选择的邻域半径成正比。对于此现象,我们可以采取折中,选取一个阈值T T T T T T
公式如下:
G ( i , j ) = { 1 L ∑ ( x , y ) ∈ A F ( x , y ) , ∣ G ( i , j ) − 1 L ∑ ( x , y ) ∈ A F ( x , y ) ∣ > T G ( i , j ) , o t h e r s G(i,j)=\left\{
\begin{array}{rcl}
\frac{1}{L}\sum\limits_{(x,y)\in A}{F(x,y)}, & & |G(i,j)-\frac{1}{L}\sum\limits_{(x,y)\in A}{F(x,y)}|>T\\
G(i,j), & & others
\end{array} \right. G ( i , j ) = { L 1 ( x , y ) ∈ A ∑ F ( x , y ) , G ( i , j ) , ∣ G ( i , j ) − L 1 ( x , y ) ∈ A ∑ F ( x , y ) ∣ > T o t h ers
频域法去噪
除了在空域内可以用空域滤波来减少视觉噪声,此外由于图像噪声频谱多分布在高频段,我们可以考虑使用低通滤波器来进行噪声滤波。
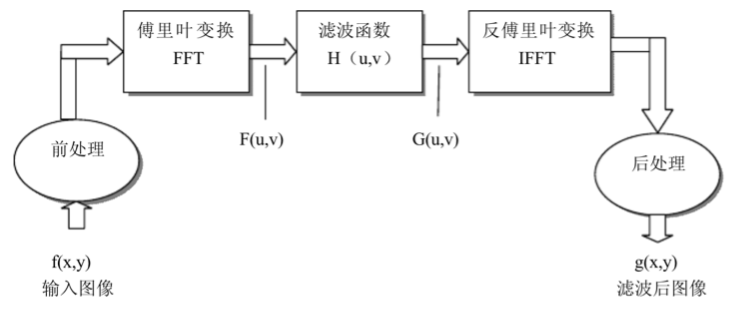
在频率域中,基本的滤波模型为:
G ( u , v ) = H ( u , v ) F ( u , v ) G(u,v)=H(u,v)F(u,v) G ( u , v ) = H ( u , v ) F ( u , v )
其中,F ( u , v ) F(u,v) F ( u , v ) H ( u , v ) H(u,v) H ( u , v ) G ( u , v ) G(u,v) G ( u , v ) H ( u , v ) H(u,v) H ( u , v ) F ( u , v ) F(u,v) F ( u , v ) G ( u , v ) G(u,v) G ( u , v ) G ( u , v ) G(u,v) G ( u , v ) g ( x , y ) g(x,y) g ( x , y )
低通滤波器常用在字符识别和印刷出版等领域,对污点、折痕和由于纸面断裂引起的字符断裂有很好的修复效果。
图像二值化算法
二值化算法,顾名思义就是将一张灰度图进行处理,将每个像素点的灰度值修改为纯白或者纯黑,即0 0 0 255 255 255
我们认为大于当前的阈值 T T T 0 0 0
图像的二值化处理可以由以下式子来进行表示:
f ( i , j ) = { 1 , f ( i , j ) ≥ T 0 , f ( i , j ) < T f(i,j)=\left\{
\begin{array}{rcl}
1, & & f(i,j) \geq T\\
0, & & f(i,j) \lt T
\end{array} \right. f ( i , j ) = { 1 , 0 , f ( i , j ) ≥ T f ( i , j ) < T
其中,T T T ( i , j ) (i,j) ( i , j ) f ( i , j ) ≥ T f(i,j) \geq T f ( i , j ) ≥ T f ( i , j ) = 1 f(i,j)=1 f ( i , j ) = 1 ( i , j ) (i,j) ( i , j ) f ( i , j ) < T f(i,j) \lt T f ( i , j ) < T f ( i , j ) = 0 f(i,j) = 0 f ( i , j ) = 0
灰度图像二值化的关键技术是阈值的选取,根据其对像素处理的方式,我们可以分为两大类算法,分别是:基于局部阈值选取的二值化算法和基于全局阈值的二值化算法。
全局阈值
全局阈值法指的是利用图像的全局信息即整体特征参数对图像求出最佳的分割点,可以是单阈值也可以是多阈值。比较典型且常用的全局阈值选取方法主要有迭代法和 Otsu 算法。
这里以 Otsu 算法为例,说明其具体原理。
Otsu 算法也被称为最大类间方差算法,以其计算简单、稳定有效,一直广为应用。算法基于类间方差的阈值选取法,它是在最小二乘函数的基础上推导出来的。
基本思想是:
取一个阈值 T T T T T T T T T
关于阈值的计算,从模式识别的角度来看,最佳阈值具有的分离性能应该能够产生最佳的目标类和背景类,此性能我们使用类别方差来描述,引入类内方差 σ A 2 \sigma_{A}^2 σ A 2 σ B 2 \sigma_{B}^2 σ B 2 σ T 2 \sigma_{T}^2 σ T 2
Q 1 = σ A 2 σ B 2 Q_{1}=\frac{\sigma_{A}^2}{\sigma_{B}^2} Q 1 = σ B 2 σ A 2
Q 2 = σ A 2 σ T 2 Q_{2}=\frac{\sigma_{A}^2}{\sigma_{T}^2} Q 2 = σ T 2 σ A 2
Q 3 = σ T 2 σ B 2 Q_{3}=\frac{\sigma_{T}^2}{\sigma_{B}^2} Q 3 = σ B 2 σ T 2
任意取一个分离指标,随后我们从 0 0 0 k m a x k_{max} k ma x Q Q Q Q Q Q T T T
通过这种全局阈值的算法,我们可以在较小计算量的情况下,通过图像快速得出一个理想的全局阈值。
但是由于文本图像普遍存在光照不均的情况,如果一份文本图像上,有些部分亮有些部分暗,阈值在选取不当的情况下就非常有可能发生将阴影背景误认为是文字导致图像出现奇怪的黑斑,将文字误认为是背景,导致一些文字显示不全残缺的情况。比较严重的时候,两者都有可能发生,说明可能让整张图使用同一个阈值效果未必很好。
下为Otsu的示例代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 int OTSU (Mat srcImage) int nCols = srcImage.cols; int nRows = srcImage.rows; int threshold = 0 ; int nSumPix[256 ]; float nProDis[256 ]; for (int i = 0 ; i < 256 ; i++) { nSumPix[i] = 0 ; nProDis[i] = 0 ; } for (int i = 0 ; i < nRows; i++) { for (int j = 0 ; j < nCols; j++) { nSumPix[(int ) srcImage.at <uchar>(i, j)]++; } } for (int i = 0 ; i < 256 ; i++) { nProDis[i] = (float ) nSumPix[i] / (nCols * nRows); } float w0, w1, u0_temp, u1_temp, u0, u1, delta_temp; double delta_max = 0.0 ; for (int i = 0 ; i < 256 ; i++) { w0 = w1 = u0 = u1 = u0_temp = u1_temp = delta_temp = 0 ; for (int j = 0 ; j < 256 ; j++) { if (j <= i) { w0 += nProDis[j]; u0_temp += j * nProDis[j]; } else { w1 += nProDis[j]; u1_temp += j * nProDis[j]; } } u0 = u0_temp / w0; u1 = u1_temp / w1; delta_temp = (float ) (w0 * w1 * pow ((u0 - u1), 2 )); if (delta_temp > delta_max) { delta_max = delta_temp; threshold = i; } } return threshold; } Mat getOtsuBinary (Mat src) { Mat srcGray; cvtColor (src, srcGray, COLOR_RGB2GRAY); Mat otsuResultImage = Mat::zeros (srcGray.rows, srcGray.cols, CV_8UC1); int otsuThreshold = OTSU (srcGray); for (int i = 0 ; i < srcGray.rows; i++) { for (int j = 0 ; j < srcGray.cols; j++) { if (srcGray.at <uchar>(i, j) > otsuThreshold) { otsuResultImage.at <uchar>(i, j) = 0 ; } else { otsuResultImage.at <uchar>(i, j) = 255 ; } } } return otsuResultImage; }
局部阈值(动态阈值)
鉴于上述问题,由于光线照射不均等因素的影响,文本图像经常会出现阴影、背景灰度不一致和图像各处目标和背景灰度值不同等情况,此时如果使用全局阈值法必然会使二值化结果受到影响,给后续的处理造成极大的困难。这就需要使用局部阈值,也称动态阈值来对图像进行分割,这类方法使用和像素位置相关的一组阈值来对图像各个局域部分分别进行分割处理。
局部阈值法是把整幅图像切分成几个小面积的子图像。再分别根据子图像应用全局阈值法求出最佳的分割阈值。显而易见的可以看出,此类方法的计算量相较于全局阈值法可能会很大,而且和局部区域的面积成正相关。
典型的局部阈值算法有 Bernsen 算法、NiBlack 算法和 Sauvola 算法。
下面以 Sauvola 算法为例,介绍其具体原理。
Sauvola 算法的输入是灰度图像,它以当前像素点为中心,根据当前像素点邻域内的灰度均值与标准方差来动态计算该像素点的阈值。
假定当前像素点的坐标为( x , y ) (x,y) ( x , y ) r × r r \times r r × r g ( x , y ) g(x,y) g ( x , y ) ( x , y ) (x,y) ( x , y )
首先计算出r × r r \times r r × r m ( x , y ) m(x,y) m ( x , y ) s ( x , y ) s(x,y) s ( x , y )
m ( x , y ) = 1 r 2 ∑ i = x − r 2 x + r 2 ∑ j = y − r 2 y + r 2 g ( i , j ) m(x,y)=\frac{1}{r^2}\sum\limits_{i=x-\frac{r}{2}}^{x+\frac{r}{2}}\sum\limits_{j=y-\frac{r}{2}}^{y+\frac{r}{2}}g(i,j) m ( x , y ) = r 2 1 i = x − 2 r ∑ x + 2 r j = y − 2 r ∑ y + 2 r g ( i , j )
s ( x , y ) = 1 r 2 ∑ i = x − r 2 x + r 2 ∑ j = y − r 2 y + r 2 ( g ( i , j ) − m ( x , y ) ) 2 s(x,y)=\sqrt{\frac{1}{r^2}\sum\limits_{i=x-\frac{r}{2}}^{x+\frac{r}{2}}\sum\limits_{j=y-\frac{r}{2}}^{y+\frac{r}{2}}(g(i,j)-m(x,y))^2} s ( x , y ) = r 2 1 i = x − 2 r ∑ x + 2 r j = y − 2 r ∑ y + 2 r ( g ( i , j ) − m ( x , y ) ) 2
接下来计算像素点( x , y ) (x,y) ( x , y ) T ( x , y ) T(x,y) T ( x , y )
T ( x , y ) = m ( x , y ) ⋅ [ 1 + k ⋅ ( s ( x , y ) R − 1 ) ] T(x,y)=m(x,y)\cdot [1+k \cdot (\frac{s(x,y)}{R}-1)] T ( x , y ) = m ( x , y ) ⋅ [ 1 + k ⋅ ( R s ( x , y ) − 1 )]
其中R R R 8 8 8 R = 128 R=128 R = 128 k k k k k k 0 < k < 1 0\lt k \lt 1 0 < k < 1
具体算法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 float fastMean (Mat &integral, int x, int y, int window) int min_y = max (0 , y - window / 2 ); int max_y = min (integral.rows - 1 , y + window / 2 ); int min_x = max (0 , x - window / 2 ); int max_x = min (integral.cols - 1 , x + window / 2 ); int topright = integral.at <int >(max_y, max_x); int botleft = integral.at <int >(min_y, min_x); int topleft = integral.at <int >(max_y, min_x); int botright = integral.at <int >(min_y, max_x); float res = (float ) ((topright + botleft - topleft - botright) / (float ) ((max_y - min_y) * (max_x - min_x))); return res; } Mat Sauvola (Mat &src, int window, float k) { Mat srcGray; cvtColor (src, srcGray, COLOR_RGB2GRAY); Mat resImg (srcGray.size(), CV_8UC1) ; Mat integral; int nYOffSet = 3 ; int nXOffSet = 3 ; cv::integral (srcGray, integral); for (int y = 0 ; y < srcGray.rows; y += nYOffSet) { for (int x = 0 ; x < srcGray.cols; x += nXOffSet) { float fmean = fastMean (integral, x, y, window); float fthreshold = (float ) (fmean * (1.0 - k)); int nNextY = y + nYOffSet; int nNextX = x + nXOffSet; int nCurY = y; while (nCurY < nNextY && nCurY < srcGray.rows) { int nCurX = x; while (nCurX < nNextX && nCurX < srcGray.cols) { uchar val = srcGray.at <uchar>(nCurY, nCurX) < fthreshold; resImg.at <uchar>(nCurY, nCurX) = (val == 0 ? 0 : 255 ); nCurX++; } nCurY++; } } } return resImg; }
P.S. 为了方便处理,二值化图像都进行了反色处理,使得文字部分更加突出了。
比较
首先使用全局阈值的 Otsu 算法,效果如下:
很明显的观察到,由于光影的变化问题,阈值的选取导致了大量的阴影区域被定义为了文字,导致了识别的困难。
而 Sauvola 算法就可以达到相对较好的效果:
注意到局部阈值的效果很大程度上也取决于我们所框选的邻域的大小,虽然在上述例子中15 × 15 15 \times 15 15 × 15
由于选取的邻域过小,导致邻域全部选在了字体内部的黑色区域中,导致了同为黑色,方差过小,全部被判定成了背景,这种情况下 Otsu 算法就会显著好于 Sauvola。
同理如果由于邻域选取过大,Otsu 等全局阈值算法的缺点也会在Sauvola算法中产生。
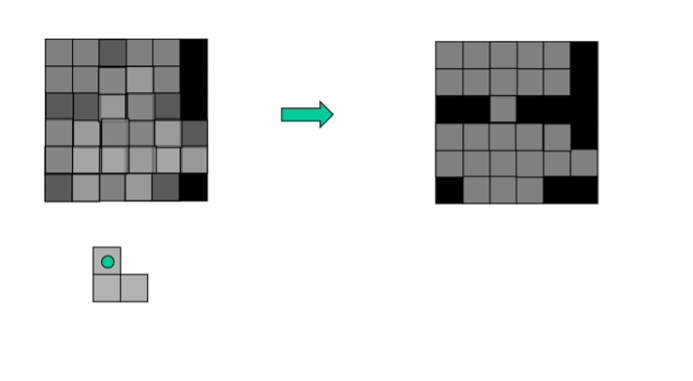
腐蚀膨胀
腐蚀和膨胀算法是数学形态学里面最常见的基本运算,将其合理结合起来使用就可以进行图像形状或者结构的分析和处理,包括边界检测、特征提取、图像分割、图像滤波等方面的工作。
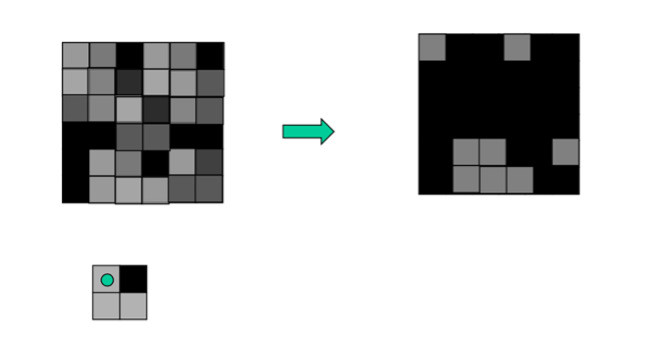
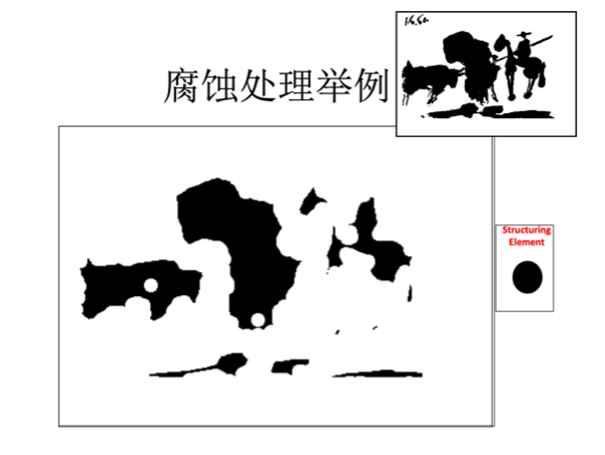
“膨胀”就是对图像中的高亮部分进行扩张,让白色区域变多;“腐蚀”就是图像中的高亮部分被蚕食,让黑色区域变多。通过膨胀、腐蚀的一系列操作,可将文字区域的轮廓突出,并消除掉一些边框线条,再通过查找轮廓的方法计算出文字区域的位置出来。
形态学开操作中,腐蚀会删除小的物体,而后续的膨胀会试图恢复遗留物体的形状。然而这种恢复的准确性高度依赖于物体的形状和所用结构元的相似性。重建开操作可正确地恢复腐蚀后所保留物体的形状。
我们可以通过腐蚀的操作,来实现消除一些边框线条。腐蚀算法的步骤如下:
扫描原图,找到第一个像素值为1的目标点;
将预先设定好形状以及原点位置的结构元素的原点移到该点;
判断该结构元素所覆盖范围内的像素值是否全部为1: 如果是,则腐蚀后图像中的相同位置上的像素值为1; 如果不是,则腐蚀后图像中的相同位置上的像素值为0;
重复 2 和 3 ,直到所有原图中像素处理完成。
随后我们在水平方向上对上述图像进行膨胀,这样操作下来所有同行的字体就会连接在一起,形成大题的行的轮廓。
膨胀的相关操作与腐蚀类似:
扫描原图,找到第一个像素值为0的背景点;
将预先设定好形状以及原点位置的结构元素的原点移到该点;
判断该结构元素所覆盖范围内的像素值是否存在为1的目标点: 如果是,则膨胀后图像中的相同位置上的像素值为1;如果不是,则膨胀后图像中的相同位置上的像素值为0;
重复 2 和 3 ,直到所有原图中像素处理完成。
我们使用刚才 Sauvola 算法的相关结果,对图像进行进一步的处理。
我们看到二值化后,图像中在左上和底部存在着部分污渍,如果在膨胀前不进行相关处理会被识别成行干扰后续处理判断。
注意到为了行连接,我们后续需要主要在水平方向上向右进行拓展膨胀。因此,我们采用水平方向的先腐蚀后拓展,将污点消去后,再对行进行整体的连接。
代码如下:
1 2 3 4 5 6 7 8 9 Mat element1 = getStructuringElement (MORPH_RECT, Size (15 , 3 )); Mat element2 = getStructuringElement (MORPH_RECT, Size (20 , 5 )); Mat element3 = getStructuringElement (MORPH_RECT, Size (30 , 3 )); Mat out; dilate (Sauvola (image, 15 , 0.3 ), out, element1);erode (out, out, element2);dilate (out, out, element3);
效果图如下:
轮廓检测
接下来,我们要针对二值化图像,进行轮廓的提取。
在这里直接使用了 OpenCV 自带的 findContours 函数完成了相关操作。
该算法通过对二值图像进行拓扑分析,确定了边界之间的包含关系,随后找出了最外层的边界。并输出了各个部分的边缘关键点,以 vector<vector<Point>>的形式保存了下来。
使用轮廓检测,调用 OpenCV 自带的findContours 方法,我们完成联通域的边缘的绘制,并且输出了关键的边缘折点。代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 vector<vector<Point>> contours; vector<Vec4i> hierarchy; findContours (out, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point ());Mat imageContours = Mat::zeros (image.size (), CV_8UC1); Mat Contours = Mat::zeros (image.size (), CV_8UC1); for (int i = 0 ; i < contours.size (); i++) { for (int j = 0 ; j < contours[i].size (); j++) { Point P = Point (contours[i][j].x, contours[i][j].y); Contours.at <uchar>(P) = 255 ; } char ch[256 ]; sprintf (ch, "%d" , i); string str = ch; drawContours (imageContours, contours, i, Scalar (255 ), 1 , 8 , hierarchy); } imshow ("out1" , imageContours);
效果如下:
最小二乘法拟合直线并确认交点
针对各个联通域的边缘关键点,我们进行提取,例如我们提取所有最右侧的关键点,即可得到一条“近似”对齐的直线,当然这里面还有很多需要排除的点,例如有些行没有延伸到本页的末尾,在这里,我们使用图像宽度的 2 3 \frac{2}{3} 3 2 1 3 \frac{1}{3} 3 1
同理,可以得到顶部、底部、左部边界线。
使用最小二乘法进行直线拟合。
设x x x y y y
y = a + b x y=a+bx y = a + b x
式中有两个待定参数,a a a b b b ( x i , y i ) (x_{i},y_{i}) ( x i , y i ) i = 1 , 2... , N i=1,2 ...,N i = 1 , 2... , N x i x_{i} x i y i y_{i} y i
用最小二乘法估计参数时,要求观测值y i y_{i} y i
∑ i = 1 N [ y i − ( a + b x i ) ] 2 \sum\limits_{i=1}^{N}[y_{i}-(a+bx_{i})]^2 i = 1 ∑ N [ y i − ( a + b x i ) ] 2
代码如下:
传入点集为points,我们会在image中绘制拟合直线,并将直线上的点以vector<Point>的形式加入到edges中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 Mat fitLineByRegression (vector<Point> points, Mat image, vector<vector<Point>>& edges) { Mat src = image.clone (); for (int i = 0 ; i < points.size (); i++) { circle (src, points[i], 3 , Scalar (0 , 0 , 255 ), 1 , 8 ); } int N = 2 ; Mat A = Mat::zeros (N, N, CV_64FC1); for (int row = 0 ; row < A.rows; row++) { for (int col = 0 ; col < A.cols; col++) { for (int k = 0 ; k < points.size (); k++) { A.at <double >(row, col) = A.at <double >(row, col) + pow (points[k].x, row + col); } } } Mat B = Mat::zeros (N, 1 , CV_64FC1); for (int row = 0 ; row < B.rows; row++) { for (int k = 0 ; k < points.size (); k++) { B.at <double >(row, 0 ) = B.at <double >(row, 0 ) + pow (points[k].x, row) * points[k].y; } } Mat X; solve (A, B, X, DECOMP_LU); cout << X << endl; vector<Point> lines; for (int x = 0 ; x < src.size ().width; x++) { double y = X.at <double >(0 , 0 ) + X.at <double >(1 , 0 ) * x; printf ("(%d,%lf)\n" , x, y); lines.push_back (Point (x, y)); } edges.push_back (lines); polylines (src, lines, false , Scalar (255 , 0 , 0 ), 1 , 8 ); return src; }
关于如何确定上下左右四条线的点集,逻辑代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 vector<Point2f> getCorners (Mat src) { vector<vector<Point>> contours; vector<Vec4i> hierarchy; findContours (src, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point ()); vector<Point> top, bottom, left, right; int top_flag = -1 , bottom_flag = -1 ; int top_val = src.rows, bottom_val = 0 ; for (int i = 0 ; i < contours.size (); i++) { Point most_left = Point (src.cols, 0 ); Point most_right = Point (-1 , 0 ); for (Point point: contours[i]) { if (point.x > most_right.x) { most_right = point; } if (point.x < most_left.x) { most_left = point; } if (point.y < top_val) { top_flag = i; top_val = point.y; } if (point.y > bottom_val){ bottom_flag = i; bottom_val = point.y; } } if (most_left.x < src.cols / 3 ) left.push_back (most_left); if (most_right.x > src.cols * 2 / 3 ) right.push_back (most_right); } top = contours[top_flag]; bottom = contours[bottom_flag]; }
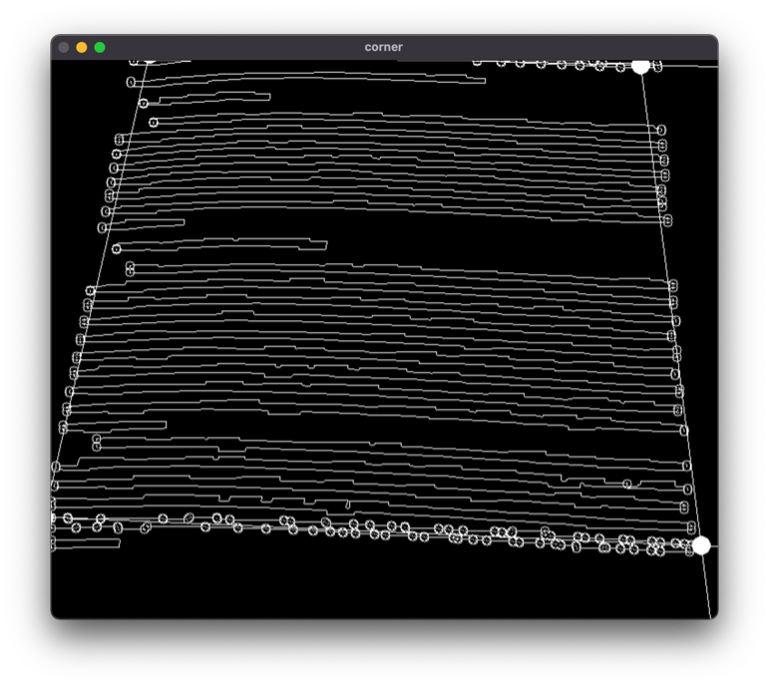
拟合直线结果如下:
我们使用如下函数确定两条直线的交点,其中LineA和LineB内部存储的都是直线上面所包含的点集:
1 2 3 4 5 6 7 8 9 10 11 12 Point2f getCrossPoint (vector<Point> LineA, vector<Point> LineB) double ka, kb; int lenA = LineA.size (), lenB = LineB.size (); ka = (double )(LineA[lenA - 1 ].y - LineA[0 ].y) / (double )(LineA[lenA - 1 ].x - LineA[0 ].x); kb = (double )(LineB[lenB - 1 ].y - LineB[0 ].y) / (double )(LineB[lenB - 1 ].x - LineB[0 ].x); Point2f crossPoint; crossPoint.x = (ka*LineA[0 ].x - LineA[0 ].y - kb*LineB[0 ].x + LineB[0 ].y) / (ka - kb); crossPoint.y = (ka*kb*(LineA[0 ].x - LineB[0 ].x) + ka*LineB[0 ].y - kb*LineA[0 ].y) / (ka - kb); return crossPoint; }
通过这样的方法,我们绘制出了四个边角,并得到了其相应的坐标。
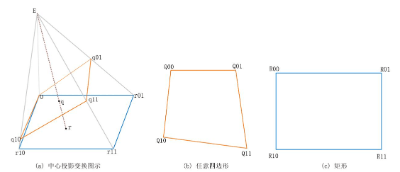
透视畸变矫正
由于相机制造精度以及组装工艺的偏差引入的畸变,或者由于照片拍摄时的角度、旋转、缩放等问题, 可能会导致原始图像的失真,如果要修复这些失真,我们可以通过透视变换,对图像进行畸变矫正。
通用的变换公式为:
[ X Y Z ] = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] [ x y 1 ] \begin{bmatrix}X\\Y\\Z\end{bmatrix}=\begin{bmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} X Y Z = a 11 a 21 a 31 a 12 a 22 a 32 a 13 a 23 a 33 x y 1
( X , Y , Z ) (X,Y,Z) ( X , Y , Z ) ( X ′ , Y ′ , Z ′ ) (X',Y',Z') ( X ′ , Y ′ , Z ′ ) Z ′ = 1 Z'=1 Z ′ = 1 Z ′ Z' Z ′
{ X ′ = X Z Y ′ = Y Z Z ′ = Z Z \left\{
\begin{array}{rcl}
X'=\frac{X}{Z}\\
Y'=\frac{Y}{Z}\\Z'=\frac{Z}{Z}\end{array} \right. ⎩ ⎨ ⎧ X ′ = Z X Y ′ = Z Y Z ′ = Z Z
{ X ′ = a 11 + a 12 y + a 13 a 31 + a 32 y + a 33 Y ′ = a 21 + a 22 y + a 23 a 31 + a 32 y + a 33 Z ′ = 1 \left\{
\begin{array}{rcl}
X'=\frac{a_{11}+a_{12}y+a_{13}}{a_{31}+a_{32}y+a_{33}}\\
Y'=\frac{a_{21}+a_{22}y+a_{23}}{a_{31}+a_{32}y+a_{33}}\\ Z'=1\end{array} \right. ⎩ ⎨ ⎧ X ′ = a 31 + a 32 y + a 33 a 11 + a 12 y + a 13 Y ′ = a 31 + a 32 y + a 33 a 21 + a 22 y + a 23 Z ′ = 1
一般的,我们令a 33 = 1 a_{33}=1 a 33 = 1
{ a 11 x + a 12 y + a 13 − a 31 x X ′ − a 32 X ′ y = X ′ a 21 x + a 22 y + a 23 − a 31 x Y ′ − a 32 y Y ′ = Y ′ \left\{
\begin{array}{rcl}
a_{11}x+a_{12}y+a_{13}-a_{31}xX'-a_{32}X'y=X'\\
a_{21}x+a_{22}y+a_{23}-a_{31}xY'-a_{32}yY'=Y'\end{array} \right. { a 11 x + a 12 y + a 13 − a 31 x X ′ − a 32 X ′ y = X ′ a 21 x + a 22 y + a 23 − a 31 x Y ′ − a 32 y Y ′ = Y ′
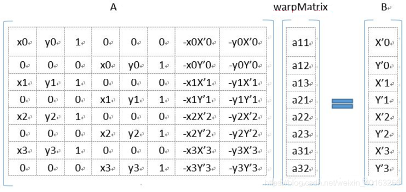
方程中共有8个未知数(a i j a_{ij} a ij
即四个点对,我们就可以解出一个变换矩阵,从而通过变换矩阵,完成相应操作。
具体算法如下:
其中pts_src为需要矫正的图上点坐标集合,pts_dst为转换后的对应点坐标。两个集合的大小都应为4,也就是总共4个点对。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Mat TransforMatrix (vector<Point2f>& pts_src,vector<Point2f>& pts_dst, Mat src, int m_dstWidth, int m_dstHeight) Mat m_MapMatrix; m_MapMatrix = getPerspectiveTransform (pts_src, pts_dst); cout << 1 << endl; Mat dst; warpPerspective (src, dst, m_MapMatrix, Size (m_dstWidth, m_dstHeight), INTER_LINEAR , BORDER_REPLICATE); return dst; }
我们将图片投射到500 × 500 500 \times 500 500 × 500
1 2 3 4 5 6 7 8 9 vector<Point2f> screen = getCorners (imageContours); vector<Point2f> now; now.push_back (Point2f (0 , 0 )); now.push_back (Point2f (500 , 0 )); now.push_back (Point2f (0 , 500 )); now.push_back (Point2f (500 , 500 )); cout << screen.size () << endl; cout << now.size () << endl; imshow ("final" , TransforMatrix (screen, now, image, 500 , 500 ));
结果如下:
和原图对比,在一定程度下完成了透视畸变的矫正。
最终的全部代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 401 402 #include "opencv2/highgui.hpp" #include <opencv2/opencv.hpp> using namespace std;using namespace cv;Mat AverFiltering (Mat &src) { Mat dst (src.size(), src.type()) ; if (!src.data) return dst; for (int i = 1 ; i < src.rows; ++i) { for (int j = 1 ; j < src.cols; ++j) { if ((i - 1 >= 0 ) && (j - 1 ) >= 0 && (i + 1 ) < src.rows && (j + 1 ) < src.cols) { dst.at <Vec3b>(i, j)[0 ] = (src.at <Vec3b>(i, j)[0 ] + src.at <Vec3b>(i - 1 , j - 1 )[0 ] + src.at <Vec3b>(i - 1 , j)[0 ] + src.at <Vec3b>(i, j - 1 )[0 ] + src.at <Vec3b>(i - 1 , j + 1 )[0 ] + src.at <Vec3b>(i + 1 , j - 1 )[0 ] + src.at <Vec3b>(i + 1 , j + 1 )[0 ] + src.at <Vec3b>(i, j + 1 )[0 ] + src.at <Vec3b>(i + 1 , j)[0 ]) / 9 ; dst.at <Vec3b>(i, j)[1 ] = (src.at <Vec3b>(i, j)[1 ] + src.at <Vec3b>(i - 1 , j - 1 )[1 ] + src.at <Vec3b>(i - 1 , j)[1 ] + src.at <Vec3b>(i, j - 1 )[1 ] + src.at <Vec3b>(i - 1 , j + 1 )[1 ] + src.at <Vec3b>(i + 1 , j - 1 )[1 ] + src.at <Vec3b>(i + 1 , j + 1 )[1 ] + src.at <Vec3b>(i, j + 1 )[1 ] + src.at <Vec3b>(i + 1 , j)[1 ]) / 9 ; dst.at <Vec3b>(i, j)[2 ] = (src.at <Vec3b>(i, j)[2 ] + src.at <Vec3b>(i - 1 , j - 1 )[2 ] + src.at <Vec3b>(i - 1 , j)[2 ] + src.at <Vec3b>(i, j - 1 )[2 ] + src.at <Vec3b>(i - 1 , j + 1 )[2 ] + src.at <Vec3b>(i + 1 , j - 1 )[2 ] + src.at <Vec3b>(i + 1 , j + 1 )[2 ] + src.at <Vec3b>(i, j + 1 )[2 ] + src.at <Vec3b>(i + 1 , j)[2 ]) / 9 ; } else { dst.at <Vec3b>(i, j)[0 ] = src.at <Vec3b>(i, j)[0 ]; dst.at <Vec3b>(i, j)[1 ] = src.at <Vec3b>(i, j)[1 ]; dst.at <Vec3b>(i, j)[2 ] = src.at <Vec3b>(i, j)[2 ]; } } } return dst; } Mat Sharpen (Mat &input, int percent, int type) { Mat result; Mat s = input.clone (); Mat kernel; switch (type) { case 0 : kernel = (Mat_ <int >(3 , 3 ) << 0 , -1 , 0 , -1 , 4 , -1 , 0 , -1 , 0 ); case 1 : kernel = (Mat_ <int >(3 , 3 ) << -1 , -1 , -1 , -1 , 8 , -1 , -1 , -1 , -1 ); default : kernel = (Mat_ <int >(3 , 3 ) << 0 , -1 , 0 , -1 , 4 , -1 , 0 , -1 , 0 ); } filter2D (s, s, s.depth (), kernel); result = input + s * 0.01 * percent; return result; } int OTSU (Mat srcImage) int nCols = srcImage.cols; int nRows = srcImage.rows; int threshold = 0 ; int nSumPix[256 ]; float nProDis[256 ]; for (int i = 0 ; i < 256 ; i++) { nSumPix[i] = 0 ; nProDis[i] = 0 ; } for (int i = 0 ; i < nRows; i++) { for (int j = 0 ; j < nCols; j++) { nSumPix[(int ) srcImage.at <uchar>(i, j)]++; } } for (int i = 0 ; i < 256 ; i++) { nProDis[i] = (float ) nSumPix[i] / (nCols * nRows); } float w0, w1, u0_temp, u1_temp, u0, u1, delta_temp; double delta_max = 0.0 ; for (int i = 0 ; i < 256 ; i++) { w0 = w1 = u0 = u1 = u0_temp = u1_temp = delta_temp = 0 ; for (int j = 0 ; j < 256 ; j++) { if (j <= i) { w0 += nProDis[j]; u0_temp += j * nProDis[j]; } else { w1 += nProDis[j]; u1_temp += j * nProDis[j]; } } u0 = u0_temp / w0; u1 = u1_temp / w1; delta_temp = (float ) (w0 * w1 * pow ((u0 - u1), 2 )); if (delta_temp > delta_max) { delta_max = delta_temp; threshold = i; } } return threshold; } Mat getOtsuBinary (Mat src) { Mat srcGray; cvtColor (src, srcGray, COLOR_RGB2GRAY); Mat otsuResultImage = Mat::zeros (srcGray.rows, srcGray.cols, CV_8UC1); int otsuThreshold = OTSU (srcGray); for (int i = 0 ; i < srcGray.rows; i++) { for (int j = 0 ; j < srcGray.cols; j++) { if (srcGray.at <uchar>(i, j) > otsuThreshold) { otsuResultImage.at <uchar>(i, j) = 0 ; } else { otsuResultImage.at <uchar>(i, j) = 255 ; } } } return otsuResultImage; } float fastMean (Mat &integral, int x, int y, int window) int min_y = max (0 , y - window / 2 ); int max_y = min (integral.rows - 1 , y + window / 2 ); int min_x = max (0 , x - window / 2 ); int max_x = min (integral.cols - 1 , x + window / 2 ); int topright = integral.at <int >(max_y, max_x); int botleft = integral.at <int >(min_y, min_x); int topleft = integral.at <int >(max_y, min_x); int botright = integral.at <int >(min_y, max_x); float res = (float ) ((topright + botleft - topleft - botright) / (float ) ((max_y - min_y) * (max_x - min_x))); return res; } Mat Sauvola (cv::Mat &src, int window, float k) { Mat srcGray; cvtColor (src, srcGray, COLOR_RGB2GRAY); Mat resImg (srcGray.size(), CV_8UC1) ; Mat integral; int nYOffSet = 3 ; int nXOffSet = 3 ; cv::integral (srcGray, integral); for (int y = 0 ; y < srcGray.rows; y += nYOffSet) { for (int x = 0 ; x < srcGray.cols; x += nXOffSet) { float fmean = fastMean (integral, x, y, window); float fthreshold = (float ) (fmean * (1.0 - k)); int nNextY = y + nYOffSet; int nNextX = x + nXOffSet; int nCurY = y; while (nCurY < nNextY && nCurY < srcGray.rows) { int nCurX = x; while (nCurX < nNextX && nCurX < srcGray.cols) { uchar val = srcGray.at <uchar>(nCurY, nCurX) < fthreshold; resImg.at <uchar>(nCurY, nCurX) = (val == 0 ? 0 : 255 ); nCurX++; } nCurY++; } } } return resImg; } Point2f getCrossPoint (vector<Point> LineA, vector<Point> LineB) double ka, kb; int lenA = LineA.size (), lenB = LineB.size (); ka = (double )(LineA[lenA - 1 ].y - LineA[0 ].y) / (double )(LineA[lenA - 1 ].x - LineA[0 ].x); kb = (double )(LineB[lenB - 1 ].y - LineB[0 ].y) / (double )(LineB[lenB - 1 ].x - LineB[0 ].x); Point2f crossPoint; crossPoint.x = (ka*LineA[0 ].x - LineA[0 ].y - kb*LineB[0 ].x + LineB[0 ].y) / (ka - kb); crossPoint.y = (ka*kb*(LineA[0 ].x - LineB[0 ].x) + ka*LineB[0 ].y - kb*LineA[0 ].y) / (ka - kb); return crossPoint; } Mat fitLineByRegression (vector<Point> points, Mat image, vector<vector<Point>>& edges) { Mat src = image.clone (); for (int i = 0 ; i < points.size (); i++) { circle (src, points[i], 3 , Scalar (0 , 0 , 255 ), 1 , 8 ); } int N = 2 ; Mat A = Mat::zeros (N, N, CV_64FC1); for (int row = 0 ; row < A.rows; row++) { for (int col = 0 ; col < A.cols; col++) { for (int k = 0 ; k < points.size (); k++) { A.at <double >(row, col) = A.at <double >(row, col) + pow (points[k].x, row + col); } } } Mat B = Mat::zeros (N, 1 , CV_64FC1); for (int row = 0 ; row < B.rows; row++) { for (int k = 0 ; k < points.size (); k++) { B.at <double >(row, 0 ) = B.at <double >(row, 0 ) + pow (points[k].x, row) * points[k].y; } } Mat X; solve (A, B, X, DECOMP_LU); cout << X << endl; vector<Point> lines; for (int x = 0 ; x < src.size ().width; x++) { double y = X.at <double >(0 , 0 ) + X.at <double >(1 , 0 ) * x; printf ("(%d,%lf)\n" , x, y); lines.push_back (Point (x, y)); } edges.push_back (lines); polylines (src, lines, false , Scalar (255 , 0 , 0 ), 1 , 8 ); return src; } vector<Point2f> getCorners (Mat src) { vector<vector<Point>> contours; vector<Vec4i> hierarchy; findContours (src, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point ()); vector<Point> top, bottom, left, right; int top_flag = -1 , bottom_flag = -1 ; int top_val = src.rows, bottom_val = 0 ; for (int i = 0 ; i < contours.size (); i++) { Point most_left = Point (src.cols, 0 ); Point most_right = Point (-1 , 0 ); for (Point point: contours[i]) { if (point.x > most_right.x) { most_right = point; } if (point.x < most_left.x) { most_left = point; } if (point.y < top_val) { top_flag = i; top_val = point.y; } if (point.y > bottom_val){ bottom_flag = i; bottom_val = point.y; } } if (most_left.x < src.cols / 3 ) left.push_back (most_left); if (most_right.x > src.cols * 2 / 3 ) right.push_back (most_right); } top = contours[top_flag]; bottom = contours[bottom_flag]; Mat image = src.clone (); vector<vector<Point>> edges; for (Point x: left) { circle (image, x, 5 , Scalar (255 , 0 , 0 ), 1 , 8 ); } image = fitLineByRegression (left, image, edges); for (Point x: right) { circle (image, x, 5 , Scalar (255 , 0 , 0 ), 1 , 8 ); } image = fitLineByRegression (right, image, edges); for (Point x: top) { circle (image, x, 5 , Scalar (255 , 0 , 0 ), 1 , 8 ); } image = fitLineByRegression (top, image, edges); for (Point x: bottom) { circle (image, x, 5 , Scalar (255 , 0 , 0 ), 1 , 8 ); } image = fitLineByRegression (bottom, image, edges); imshow ("line" , image); cout << edges.size () << endl; Point lt = getCrossPoint (edges[0 ], edges[2 ]); Point rt = getCrossPoint (edges[1 ], edges[2 ]); Point lb = getCrossPoint (edges[0 ], edges[3 ]); Point rb = getCrossPoint (edges[1 ], edges[3 ]); cout << lt.x << " " << lt.y << endl; cout << lb.x << " " << lb.y << endl; cout << rt.x << " " << rt.y << endl; cout << rb.x << " " << rb.y << endl; circle (image, lt, 5 , Scalar (255 , 0 , 0 ), 10 , 8 ); circle (image, lb, 5 , Scalar (255 , 0 , 0 ), 10 , 8 ); circle (image, rb, 5 , Scalar (255 , 0 , 0 ), 10 , 8 ); circle (image, rt, 5 , Scalar (255 , 0 , 0 ), 10 , 8 ); imshow ("corner" , image); vector<Point2f> res; res.push_back (lt); res.push_back (rt); res.push_back (lb); res.push_back (rb); return res; } Mat TransforMatrix (vector<Point2f>& pts_src,vector<Point2f>& pts_dst, Mat src, int m_dstWidth, int m_dstHeight) Mat m_MapMatrix; m_MapMatrix = getPerspectiveTransform (pts_src, pts_dst); cout << 1 << endl; Mat dst; warpPerspective (src, dst, m_MapMatrix, Size (m_dstWidth, m_dstHeight), INTER_LINEAR , BORDER_REPLICATE); return dst; } int main () Mat image = imread ("/Users/ray/Downloads/题目4/t4.jpg" ); imshow ("origin" , image); imshow ("average" , AverFiltering (image)); imshow ("otsu" , getOtsuBinary (image)); imshow ("sauvola" , Sauvola (image, 15 , 0.3 )); Mat element1 = getStructuringElement (MORPH_RECT, Size (15 , 3 )); Mat element2 = getStructuringElement (MORPH_RECT, Size (20 , 5 )); Mat element3 = getStructuringElement (MORPH_RECT, Size (30 , 3 )); Mat out; dilate (Sauvola (image, 15 , 0.3 ), out, element1); erode (out, out, element2); dilate (out, out, element3); vector<vector<Point>> contours; vector<Vec4i> hierarchy; findContours (out, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point ()); Mat imageContours = Mat::zeros (image.size (), CV_8UC1); Mat Contours = Mat::zeros (image.size (), CV_8UC1); for (int i = 0 ; i < contours.size (); i++) { for (int j = 0 ; j < contours[i].size (); j++) { Point P = Point (contours[i][j].x, contours[i][j].y); Contours.at <uchar>(P) = 255 ; } char ch[256 ]; sprintf (ch, "%d" , i); string str = ch; drawContours (imageContours, contours, i, Scalar (255 ), 1 , 8 , hierarchy); } imshow ("out" , out); imshow ("out1" , imageContours); vector<Point2f> screen = getCorners (imageContours); vector<Point2f> now; now.push_back (Point2f (0 , 0 )); now.push_back (Point2f (500 , 0 )); now.push_back (Point2f (0 , 500 )); now.push_back (Point2f (500 , 500 )); cout << screen.size () << endl; cout << now.size () << endl; imshow ("final" , TransforMatrix (screen, now, image, 500 , 500 )); waitKey (); return 0 ; }