Leetcode Bio-Weekly Contest Round 70
又是为了毕设日常心烦的几天,为了自己的开题报告有点小情绪,文献日常看不懂却又无可奈何,就很累…
也许有可能,只是有可能,我根本不适合自己这个专业,学的也累也没热情。
不牢骚了,看题去了,又是补题的一周。
T1 2144. 打折购买糖果的最小开销
题目
一家商店正在打折销售糖果。每购买 两个 糖果,商店会 免费 送一个糖果。
免费送的糖果唯一的限制是:它的价格需要小于等于购买的两个糖果价格的 较小值 。
比方说,总共有 4 个糖果,价格分别为 1 ,2 ,3 和 4 ,一位顾客买了价格为 2 和 3 的糖果,那么他可以免费获得价格为 1 的糖果,但不能获得价格为 4 的糖果。
给你一个下标从 0 开始的整数数组 cost ,其中 cost[i] 表示第 i 个糖果的价格,请你返回获得 所有 糖果的 最小 总开销。
示例 1:
输入:cost = [1,2,3]
输出:5解释:我们购买价格为 2 和 3 的糖果,然后免费获得价格为 1 的糖果。
总开销为 2 + 3 = 5 。这是开销最小的 唯一 方案。
注意,我们不能购买价格为 1 和 3 的糖果,并免费获得价格为 2 的糖果。
这是因为免费糖果的价格必须小于等于购买的 2 个糖果价格的较小值。
示例 2:
输入:cost = [6,5,7,9,2,2]
输出:23解释:最小总开销购买糖果方案为:
- 购买价格为 9 和 7 的糖果
- 免费获得价格为 6 的糖果
- 购买价格为 5 和 2 的糖果
- 免费获得价格为 2 的最后一个糖果
因此,最小总开销为 9 + 7 + 5 + 2 = 23 。
示例 3:
输入:cost = [5,5]
输出:10解释:由于只有 2 个糖果,我们需要将它们都购买,而且没有免费糖果。
所以总最小开销为 5 + 5 = 10 。
提示:
题解
贪心,尽量省掉尽量大数值的糖果价格。为了做到这一点,我们直接对数组进行逆序排序,用0和1号糖果省下2号糖果,用3和4号糖果省下5号糖果的钱… 以此类推。
代码实现也比较简单:
1 | func minimumCost(cost []int) int { |
Golang自定义排序
在Java中,如果我们需要对集合进行排序,我们直接使用Collections.sort()方法即可;如果对数组进行排序,我们使用Arrays.sort()方法即可。如果需要使用自定义排序,我们只需要重写Comparator下的compare()方法,也就是比较方法,来实现集合或者数组按照我们的想法进行重新排序。为了简化写法我们还可以引入Lambda表达式。
例如:
1 | import java.util.ArrayList; |
之前对Golang的自定义排序也是一个一知半解的程度,这次好好看一下Golang内部是怎么实现排序的。
排序切片
对于[]int,[]float,[]string这类元素类型构成的切片,我们可以直接使用下方sort包内提供的函数:
sort.Intssort.Floatssort.Strings
例如:
1 | s := []int{5, 4, 3, 2, 1} |
以sort.Ints为例,我们来观察他是怎么实现的。
他是由sort包下的Ints函数来完成的,而内部又是通过Sort函数传入了一个由切片包装的IntSlice类型对象完成的:

接下来,我们先观察IntSlice对象的构成,这个IntSlice其实是接口Interface的实现,具体方法如下所示:

我们主要能够确定其中的部分功能是:
Len()返回切片长度Less(i, j int)作为比较函数,返回下表i和j处的比较结果Swap(i, j int)实现将下标i和j的元素进行交换的操作
这几个方法也算是完成一个排序的几点要素了。
与IntSlice类似,StringSlice,Float64Slice也是接口Interface的实现,Interface功能如下:

总结一下,Interface接口其实就是对切片或者集合的一个包装,他内部除了存储集合自身的数据,还定义了长度、比较和交换等操作。
回到sort.Ints的实现上,sort包下的Sorts方法是这样的:
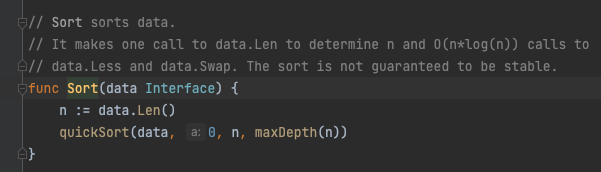
Sort()方法其实就是根据传入的Interface类型内部的数据、比较函数和交换操作等信息,对数据直接进行了相关的排序操作。我们看到他传入了一个Interface类型的切片包装,然后调用了quickSort方法,这是个快速排序的方法:
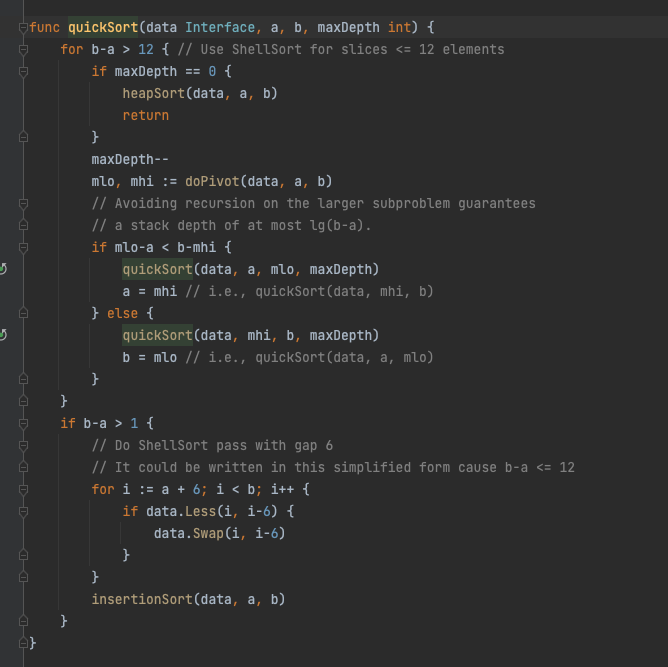
根据注释,Golang在不同的情形下还引入了优化使用了堆排序,插入排序,希尔排序等,也可以在源代码中体现出来。通过以上操作,我们以IntSlice为例认识了sort.Int()的实现方式,其他几个方法也是类似的实现逻辑。
逆序排序
在刚才的例题中,我们使用了sort.Sort(sort.Reverse(sort.IntSlice(cost)))来实现对cost数组的逆序排序,那么这又是怎么实现的呢?
里层sort.IntSlice(cost)实现了对cost的包装,随后sort.Reverse()将传入的包装好的IntSlice进行了二次包装,重写了Less()函数,生成了一个reverse的数据类型:
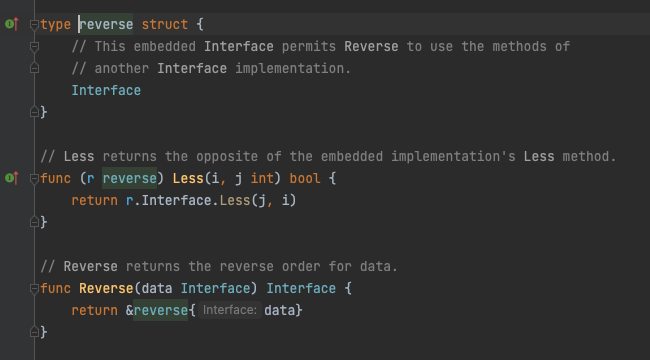
我们看到reverse也是Interface接口的一个实现,通过Reverse()方法,对Less(i, j int)函数进行了对调输出。
最后我们调用Sort()函数,根据数据和新的比较规则进行排序,完成逆序排序。
切片自定义排序
我们可以使用这样的方法进行自定义的切片排序:
1 | package main |
从使用的角度上,我们第一个参数传入切片自身,第二个参数传入我们需要自定义的Less比较函数,就可以完成自定义排序了。
首先我们观察sort包下的Slice方法:
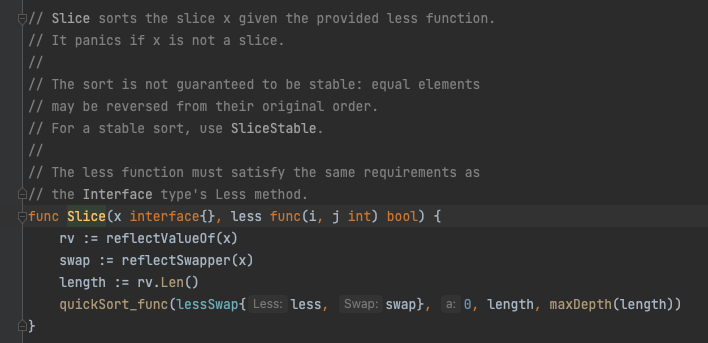
这里Golang通过反射的方式直接取出了x的数据和交换方法,随后将less函数和swap交换方法封装成lessSwap数据类型:
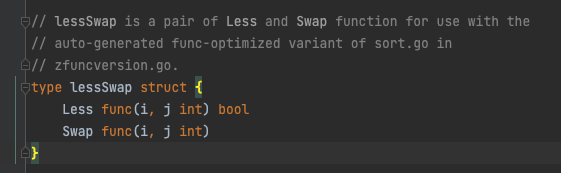
和我们的猜想相似的,quickSort_func正是通过传入的相关信息进行了自定义排序操作:
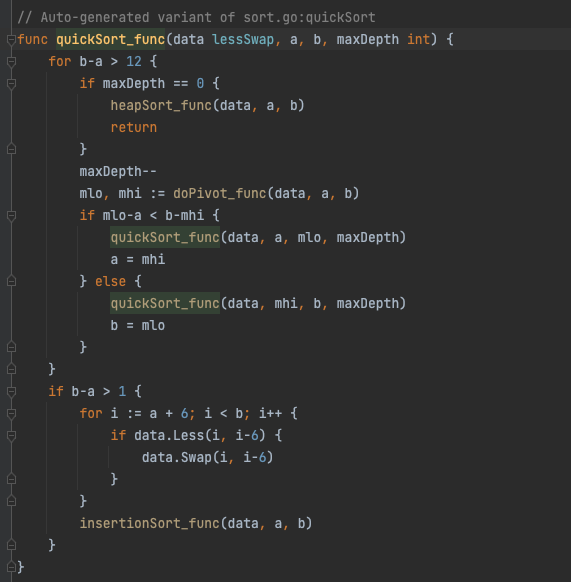
P.S. 值得注意的是,除开
sort.Slice(),Golang还另外实现了sort.SliceStable(),两者的区别是sort.SliceStable在排序切片时会保留相等元素的原始顺序,可以继续观摩一下源码。
排序任意数据结构
首先和上方的方法相似,我们可以使用sort.Sort()或者sort.Stable()来完成相关的操作。
其实差别也不大,只是这次我们需要自己创建一个类型并实现刚才说过的Interface接口。换句话说,我们需要确定三个部分:序列的长度,表示两个元素比较的结果,交换两个元素的方式。
有了刚才的铺垫,应该学着写起来不是太困难,示例如下:
1 | type Person struct { |
T2 2145. 统计隐藏数组数目
题目
给你一个下标从 0 开始且长度为 n 的整数数组 differences ,它表示一个长度为 n + 1 的 隐藏 数组 相邻 元素之间的 差值 。更正式的表述为:我们将隐藏数组记作 hidden ,那么 differences[i] = hidden[i + 1] - hidden[i] 。
同时给你两个整数 lower 和 upper ,它们表示隐藏数组中所有数字的值都在 闭 区间 [lower, upper] 之间。
- 比方说,
differences = [1, -3, 4],lower = 1,upper = 6,那么隐藏数组是一个长度为4且所有值都在1和6(包含两者)之间的数组。[3, 4, 1, 5]和[4, 5, 2, 6]都是符合要求的隐藏数组。[5, 6, 3, 7]不符合要求,因为它包含大于6的元素。[1, 2, 3, 4]不符合要求,因为相邻元素的差值不符合给定数据。
请你返回 符合 要求的隐藏数组的数目。如果没有符合要求的隐藏数组,请返回 0 。
示例 1:
输入:differences = [1,-3,4], lower = 1, upper = 6
输出:2
解释:符合要求的隐藏数组为:
- [3, 4, 1, 5]
- [4, 5, 2, 6]
所以返回 2 。
示例 2:
输入:differences = [3,-4,5,1,-2], lower = -4, upper = 5
输出:4
解释:符合要求的隐藏数组为:
- [-3, 0, -4, 1, 2, 0]
- [-2, 1, -3, 2, 3, 1]
- [-1, 2, -2, 3, 4, 2]
- [0, 3, -1, 4, 5, 3]
所以返回 4 。
示例 3:
输入:differences = [4,-7,2], lower = 3, upper = 6
输出:0
解释:没有符合要求的隐藏数组,所以返回 0 。
提示:
题解
我们只知道这个数组的“变化”特性,换句话说这个数组内部各个数字之间的相对之差是不会改变的,我们可以先随意设定一个基准,然后对其随意进行平移。
例如示例1中,给出的数组[1, -3, 4],我们假定首位元素是0,即可获得如下的数组[0, 1, -2, 2],而我们可以对这个数组中的元素进行“平移”,集体加一或者减一。
换句话说,当前数组的各个数的值域分布在数轴上的“区间长度”是固定的,例如上方的数组区间落在[-2, 2]也就是长度为4的区间里,我们需要讲这个区间摆放在规定的[1, 6]的长度为5的区间里,问有多少种摆放方式,那很显然答案就是两种。
因此,我们只需要决定数组区间的宽度l和需要的上下界宽度L,答案就是L - l + 1,当然前提是L > l不然就无法摆放,答案就应该是0。
简单的代码实现如下:
1 | func numberOfArrays(differences []int, lower int, upper int) int { |
T3 2146. 价格范围内最高排名的 K 样物品
题目
给你一个下标从 0 开始的二维整数数组 grid ,它的大小为 m x n ,表示一个商店中物品的分布图。数组中的整数含义为:
-
0表示无法穿越的一堵墙。 -
1表示可以自由通过的一个空格子。 -
所有其他正整数表示该格子内的一样物品的价格。你可以自由经过这些格子。
从一个格子走到上下左右相邻格子花费 1 步。
同时给你一个整数数组 pricing 和 start ,其中 pricing = [low, high] 且 start = [row, col] ,表示你开始位置为 (row, col) ,同时你只对物品价格在 闭区间 [low, high] 之内的物品感兴趣。同时给你一个整数 k 。
你想知道给定范围 内 且 排名最高 的 k 件物品的 位置 。排名按照优先级从高到低的以下规则制定:
- 距离:定义为从
start到一件物品的最短路径需要的步数(较近 距离的排名更高)。 - 价格:较低 价格的物品有更高优先级,但只考虑在给定范围之内的价格。
- 行坐标:较小 行坐标的有更高优先级。
- 列坐标:较小 列坐标的有更高优先级。
请你返回给定价格内排名最高的 k 件物品的坐标,将它们按照排名排序后返回。如果给定价格内少于 k 件物品,那么请将它们的坐标 全部 返回。
示例 1:
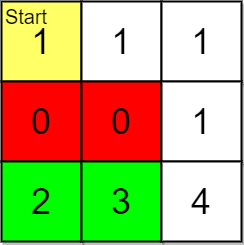
输入:grid = [[1,2,0,1],[1,3,0,1],[0,2,5,1]], pricing = [2,5], start = [0,0], k = 3
输出:[[0,1],[1,1],[2,1]]解释:起点为 (0,0) 。
价格范围为 [2,5] ,我们可以选择的物品坐标为 (0,1),(1,1),(2,1) 和 (2,2) 。
这些物品的排名为:
(0,1) 距离为 1
(1,1) 距离为 2
(2,1) 距离为 3
(2,2) 距离为 4
所以,给定价格范围内排名最高的 3 件物品的坐标为 (0,1),(1,1) 和 (2,1) 。
示例 2:
输入:grid = [[1,2,0,1],[1,3,3,1],[0,2,5,1]], pricing = [2,3], start = [2,3], k = 2
输出:[[2,1],[1,2]]解释:起点为 (2,3) 。
价格范围为 [2,3] ,我们可以选择的物品坐标为 (0,1),(1,1),(1,2) 和 (2,1) 。
这些物品的排名为:
- (2,1) 距离为 2 ,价格为 2
- (1,2) 距离为 2 ,价格为 3
- (1,1) 距离为 3
- (0,1) 距离为 4
所以,给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (1,2) 。
示例 3:
输入:grid = [[1,1,1],[0,0,1],[2,3,4]], pricing = [2,3], start = [0,0], k = 3
输出:[[2,1],[2,0]]
解释:起点为 (0,0) 。
价格范围为 [2,3] ,我们可以选择的物品坐标为 (2,0) 和 (2,1) 。
这些物品的排名为:
- (2,1) 距离为 5
- (2,0) 距离为 6
所以,给定价格范围内排名最高的 2 件物品的坐标为 (2,1) 和 (2,0) 。
注意,k = 3 但给定价格范围内只有 2 件物品。
提示:
题解
没啥,就嗯写BFS然后加上自定义排序… 当然用优先队列做大根堆那是更好的啦
只是Golang的BFS写的我有点头晕…
1 | func highestRankedKItems(grid [][]int, pricing []int, start []int, k int) [][]int { |
T4 2147. 分隔长廊的方案数
题目
在一个图书馆的长廊里,有一些座位和装饰植物排成一列。给你一个下标从 0 开始,长度为 n 的字符串 corridor ,它包含字母 'S' 和 'P' ,其中每个 'S' 表示一个座位,每个 'P' 表示一株植物。
在下标 0 的左边和下标 n - 1 的右边 已经 分别各放了一个屏风。你还需要额外放置一些屏风。每一个位置 i - 1 和 i 之间(1 <= i <= n - 1),至多能放一个屏风。
请你将走廊用屏风划分为若干段,且每一段内都 恰好有两个座位 ,而每一段内植物的数目没有要求。可能有多种划分方案,如果两个方案中有任何一个屏风的位置不同,那么它们被视为 不同 方案。
请你返回划分走廊的方案数。由于答案可能很大,请你返回它对 取余 的结果。如果没有任何方案,请返回 0 。
示例 1:
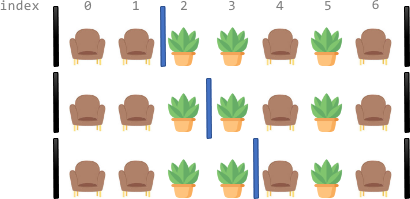
输入:corridor = “SSPPSPS”
输出:3解释:总共有 3 种不同分隔走廊的方案。
上图中黑色的竖线表示已经放置好的屏风。
上图每种方案中,每一段都恰好有 两个 座位。
示例 2:
输入:corridor = “PPSPSP”
输出:1解释:只有 1 种分隔走廊的方案,就是不放置任何屏风。
放置任何的屏风都会导致有一段无法恰好有 2 个座位。
示例 3:
输入:corridor = “S”
输出:0解释:没有任何方案,因为总是有一段无法恰好有 2 个座位。
提示:
corridor[i]要么是'S',要么是'P'。
题解
首先对于总座位数量是0或者不能被2整除的情况,很显然这样的情况下是不可能有分配方案的。
此外,如果我们把装饰植物都拿开,其实就能发现,每个屏风的相对位置都是固定的。从左向右看,座位0和座位1在一起,因此屏风必须存在在座位1和座位2之间(前提是座位2存在);座位2和座位3在一起,因此屏风必须存在在座位3和座位4之间,以此类推…
好了,直接出代码:
1 | func numberOfWays(corridor string) int { |