A*算法解决八数码问题

介绍

八数码问题

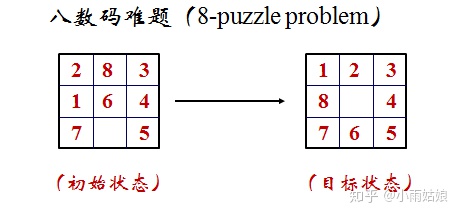
八数码问题也称为九宫问题。在3×3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格，与空格相邻的棋子可以移到空格中。要求解决的问题是：给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
所谓问题的一个状态就是棋子在棋盘上的一种摆法。棋子移动后，状态就会发生改变。解八数码问题实际上就是找出从初始状态到达目标状态所经过的一系列中间过渡状态。

A*算法

A*算法是一种启发式搜索算法，启发式搜索就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。

算法核心公式：
F = G + H
F - 决策的总代价
G - 从开始到决策时刻所花费的真实代价
H - 从决策时刻到目标的预估代价

其中G值是一个真实的代价，也就是从算法流程一开始到进行这个决策的时候，一共花费的代价。H值是一个预估的代价。在极端情况下，如果H是常量0，这个算法退化成广度优先搜索算法，即按照顺序的依次扩充每个节点。如果G是常量，这个算法退化成贪心算法，即每次扩充可以使下一次最优的节点。每次进行决策的时候，A*算法选择遍历所有当前可能的决策，并执行使F最大的决策。

open表：先能够简单认为是一个未搜索节点的表
close表：先能够简单认为是一个已完成搜索的节点的表（即已经将下一个状态放入open表内）

• 规则一：对于新添加的节点S（open表和close表中均没有这个状态），S直接添加到open表中
• 规则二：对于已经添加的节点S（open表或者close表中已经有这个状态），若在open表中，与原来的状态S0​的f(n)比较，取最小的一个。若在close表中，那就分两种状况，第一种,close表中的该状态S0​的f(n)大于S的，不作修改；第二种S0​的f(n)小于S的,那就要须要将close表中S0​的f(n)更新，同时将该状态移入到open表中。
• 规则三：下一个搜索节点的选择问题，选取open表中f(n)的值最小的状态做为下一个待搜索节点
• 规则四：每次须要将带搜索的节点下一个全部的状态按照规则一二更新open表,close表，搜索完该节点后，移到close表中。

策略

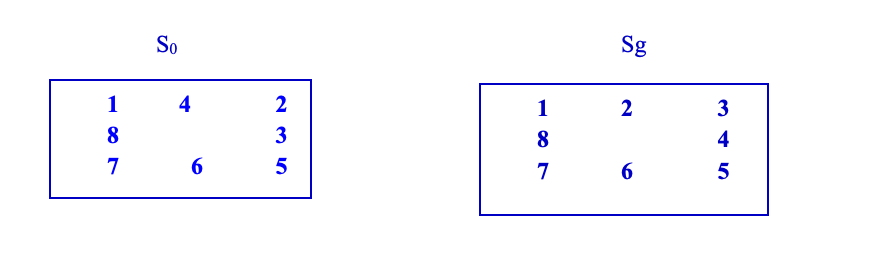
我们定义从开始状态执行的总步数为真实代价G，而当前状态与最终结果的格数差异我们记为H即从决策时刻到目标的预估代价。例如上图所示中的初始状态与最终状态之间相距了5个位置，即$H = 5$

代码解决

对于八数码问题，我们先考虑到的是如何使用数据结构将各个状态一一对应的表达出来
例如

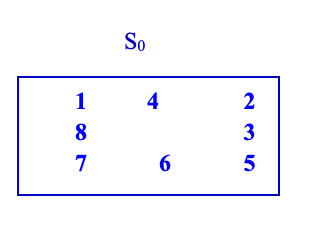
我们看到八数码问题中有9个元素的位置，我们按照行将其标记为0, 1, 2, 3, 4, 5, 6, 7, 8个元素，每个位置的元素n满足$0 \leq n \leq 8$，我们定义空位置为0
而最大8的极端情况下其二进制表达为8_D = (1000)_B，需要4位的二进制空间，则9个元素总共需要$4 * 9 = 36$位的二进制数来表示一个状态，故我们需要长整型long来进行表示

对于上图其十进制对应状态表达为1 4 2 8 0 3 7 6 5
二进制表达为 0001 0100 0010 1000 0000 0011 0111 0110 0101，记为一个32位的整型

代码如下：

import java.util.Arrays;
import java.util.HashSet;
import java.util.PriorityQueue;
import java.util.Set;

public class grid {
    Map<Long, Long> close = new HashMap<>();
    Set<Long> open = new HashSet<>();
    int[][] adjacency = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4, 6}, {1, 3, 5, 7}, {2, 4, 8}, {3, 7}, {4, 6, 8}, {5, 7}}; 
    //adjacency数组用于表示第i个元素若为空，他可以和adjacency[i]内部的元素进行交换
    public long convert(int[] arr){   //将arr数组表示为32位整型long
        long res = 0l;
        for(int i = 0; i < 9; i++){
            res += arr[i] * (1l << (i * 4));
        }
        return res;
    }
    public int diff(long stat1, long stat2){ 
        //计算stat1与stat2之间的距离差距，用于计算当前状态与目标状态之间的距离H
        int cnt = 0;
        for(int i = 0; i < 9; i++){
            long tmp1 = (stat1 >> (i * 4)) % 16;
            long tmp2 = (stat2 >> (i * 4)) % 16;
            if(tmp1 != tmp2) cnt++;
        }
        return cnt;
    }
    public long swap(long stat, int pos1, int pos2){ 
        //对于状态stat，若pos1所在位置位空（记为0），将其与pos2位置进行交换，并返回新的状态
        long tmp2 = (stat >> (pos2 * 4)) % 16; //取出pos2位置的元素
        stat -= tmp2 * (1l << (pos2 * 4));  //将pos2对应位置清0
        stat += tmp2 * (1l << (pos1 * 4));  //将0对应位置填充为pos2原先的值，完成交换
        return stat;
    }
    public int AStarSearch(int[] start, int[] target){
        int zero = -1;
        for(int i = 0; i < 9; i++){
            if(start[i] == 0) zero = i;  //标记start数组中0的位置
        }
        long a = convert(start), b = convert(target); //转换为整型状态
        PriorityQueue<long[]> pq = new PriorityQueue<>((o1, o2) -> (int) (diff(o1[1], b) + o1[2] - diff(o2[1], b) - o2[2]));
        //pq存储OPEN内部状态（可能有重复，需要根据OPEN表去重）
        //pq内部数组定义：{0的位置, 当前状态整型, 真实步数}
        pq.offer(new long[]{zero, a, 0l}); //优先队列加入初始状态
        open.add(a);
        while(!open.isEmpty()){
            long[] cur = pq.poll();
            if(!open.contains(cur[1])) continue;
            else open.remove(cur[1]);
            display(cur, b);
            if(cur[1] == b) return (int)cur[2];
            close.put(cur[1], diff(cur[1], b) + cur[2]);
            int blank = (int)cur[0];
            for(int x: adjacency[blank]) {
                long n_stat = swap(cur[1], blank, x);
                if(!close.containsKey(n_stat)){
                    open.add(n_stat);
                    pq.offer(new long[]{x, n_stat, cur[2] + 1});
                    //更新OPEN表中的估价值，加入pq
                }
                else if(cur[2] + 1 + diff(n_stat, b) < close.get(n_stat)){ 
                    //估价值小于CLOSE表的估价值 
                    close.remove(n_stat);
                    open.add(n_stat);
                    pq.offer(new long[]{x, n_stat, cur[2] + 1}); 
                    //更新CLOSE表中的估价值，从CLOSE表中移出节点，并放入OPEN表中
                }
            }
        }
        return -1; //找不到返回-1
    }

    private void display(long[] cur, long target) { //打印数组的相关信息
        int[][] res = new int[3][3];
        long stat = cur[1];
        for(int i = 0; i < 9; i++){
            res[i / 3][i % 3] = (int) (stat % 16);
            stat = stat >> 4;
        }
        for(int[] x: res) System.out.println(Arrays.toString(x)); //打印数组
        System.out.println("steps: " + cur[2]); //打印当前步数
        System.out.println("distance: " + diff(cur[1], target)); //打印与目标距离
    }

    public static void main(String[] args) {
        int[] start = new int[]{1, 4, 2, 8, 0, 3, 7, 6, 5};
        int[] target = new int[]{1, 2, 3, 8, 0, 4, 7, 6, 5};
        System.out.println("\nSTEP: " + new grid().AStarSearch(start, target));
    }
}

每一轮while循环，程序都将打印出队的cur数组相关信息，最后打印STEP最终步数
运行结果如下：

/Users/ray/Library/Java/JavaVirtualMachines/openjdk-15.0.2/Contents/Home/bin/java -javaagent:/Users/ray/Library/Application Support/JetBrains/Toolbox/apps/IDEA-U/ch-0/211.7142.45/IntelliJ IDEA.app/Contents/lib/idea_rt.jar=50003:/Users/ray/Library/Application Support/JetBrains/Toolbox/apps/IDEA-U/ch-0/211.7142.45/IntelliJ IDEA.app/Contents/bin -Dfile.encoding=UTF-8 -classpath /Users/ray/IdeaProjects/oj/out/production/oj com.company.grid
[1, 4, 2]
[8, 0, 3]
[7, 6, 5]
steps: 0
distance: 3
[1, 0, 2]
[8, 4, 3]
[7, 6, 5]
steps: 1
distance: 4
[1, 4, 2]
[8, 3, 0]
[7, 6, 5]
steps: 1
distance: 4
[1, 2, 0]
[8, 4, 3]
[7, 6, 5]
steps: 2
distance: 3
[1, 2, 3]
[8, 4, 0]
[7, 6, 5]
steps: 3
distance: 2
[1, 2, 3]
[8, 0, 4]
[7, 6, 5]
steps: 4
distance: 0

STEP: 4

Process finished with exit code 0

我们得到最终步数为4