Leetcode Weekly Contest Round 252
T1 5830. 三除数
题目
给你一个整数 n 。如果 n 恰好有三个正除数 ,返回 true ;否则,返回 false 。
如果存在整数 k ,满足 n = k * m ,那么整数 m 就是 n 的一个 除数 。
示例 1:
输入:n = 2
输出:false
解释:2 只有两个除数:1 和 2 。
示例 2:
输入:n = 4
输出:true
解释:4 有三个除数:1、2 和 4 。
提示:
题解
就…没啥,随便写
1 | class Solution { |
T2 5831. 你可以工作的最大周数
题目
给你 n 个项目,编号从 0 到 n - 1 。同时给你一个整数数组 milestones ,其中每个 milestones[i] 表示第 i 个项目中的阶段任务数量。
你可以按下面两个规则参与项目中的工作:
- 每周,你将会完成 某一个 项目中的 恰好一个 阶段任务。你每周都 必须 工作。
- 在 连续的 两周中,你 不能 参与并完成同一个项目中的两个阶段任务。
一旦所有项目中的全部阶段任务都完成,或者仅剩余一个阶段任务都会导致你违反上面的规则,那么你将 停止工作 。注意,由于这些条件的限制,你可能无法完成所有阶段任务。
返回在不违反上面规则的情况下你 最多 能工作多少周。
示例 1:
输入:milestones = [1,2,3]
输出:6解释:一种可能的情形是:
第 1 周,你参与并完成项目 0 中的一个阶段任务。
第 2 周,你参与并完成项目 2 中的一个阶段任务。
第 3 周,你参与并完成项目 1 中的一个阶段任务。
第 4 周,你参与并完成项目 2 中的一个阶段任务。
第 5 周,你参与并完成项目 1 中的一个阶段任务。
第 6 周,你参与并完成项目 2 中的一个阶段任务。
总周数是 6 。
示例 2:
输入:milestones = [5,2,1]
输出:7
解释:一种可能的情形是:第 1 周,你参与并完成项目 0 中的一个阶段任务。
第 2 周,你参与并完成项目 1 中的一个阶段任务。
第 3 周,你参与并完成项目 0 中的一个阶段任务。
第 4 周,你参与并完成项目 1 中的一个阶段任务。
第 5 周,你参与并完成项目 0 中的一个阶段任务。
第 6 周,你参与并完成项目 2 中的一个阶段任务。
第 7 周,你参与并完成项目 0 中的一个阶段任务。
总周数是 7 。
注意,你不能在第 8 周参与完成项目 0 中的最后一个阶段任务,因为这会违反规则。
因此,项目 0 中会有一个阶段任务维持未完成状态。
提示:
题解
妈耶,就很迷,写了两把都WA了
提示 1
考虑耗时最长的工作。假设我们需要 longest 周完成该工作,其余工作共计需要 rest 周完成。那么可以完成所有工作的充要条件是:
提示 1 解释
首先考虑充分性。充分性可以通过证明逆否命题,即「如果 ,那么无法完成所有的工作」,来证明。
我们可以利用反证法,如果可以完成所有工作,那么耗时最长的工作一定可以完成,这意味着至少需要有 周剩余工作可以被分配在间隔内,但剩余工作的工时 并不满足这一要求,因此充分性得证。
随后考虑必要性。必要性可以通过构造分配方案来证明。我们可以将分配工作时间的过程转化为在 闭区间内分配整数的过程,其中每个整数代表对应的一周时间。在分配整数的过程中,我们首先按照从小到大的顺序分配所有的奇数,然后按照从小到大的顺序分配所有的偶数。
我们将所有工作按照耗时从高到低来排序,按照前文的顺序分配对应的时间。此时由于,因此耗时最长的工作不会出现任意两周相邻这种违反规定的情况。类似地可以证明,其他工作由于耗时小于最长的工作,也不会出现相邻的情况。因此必要性得证。
思路与算法
根据 提示 1,我们首先计算出耗时最长的工作所需周数 与剩余工作所需周数 ,并比较两者大小。根据比较的结果不同会有两种情况:
- ,此时根据 提示 1,所有工作都可以完成,我们返回所有工作的总耗时 作为答案。
- ,此时我们无法完成耗时最长的工作。根据 提示 1 的证明过程,耗时最长的工作最多可以完成 周,因此最大的工作周数即为 ,我们返回该数作为答案。
最后,由于 可能超过 32 位整数的范围,我们需要使用 64 位整数进行相应的计算与比较。
1 | class Solution { |
复杂度分析
时间复杂度:,其中 n 为 milestones 的长度。即为遍历数组计算耗时总和与最大值的时间复杂度。
空间复杂度:。
总之就是个挺玄学的贪心?本人写的垃圾代码在此。。。也算是差不多的思路啦
1 | class Solution { |
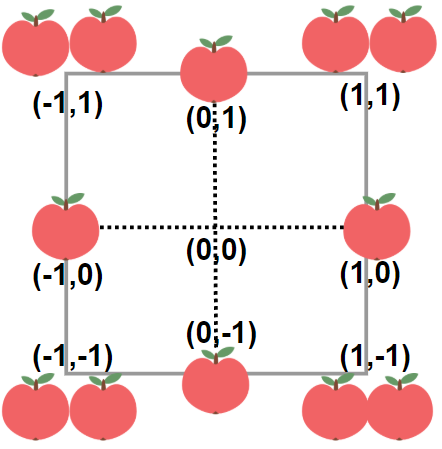
T3 5187. 收集足够苹果的最小花园周长
题目
给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。
你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ,且每条边都与两条坐标轴之一平行。
给你一个整数 neededApples ,请你返回土地的 最小周长 ,使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。
|x| 的值定义为:
如果 x >= 0 ,那么值为 x
如果 x < 0 ,那么值为 -x
示例 1:
输入:neededApples = 1
输出:8
解释:边长长度为 1 的正方形不包含任何苹果。
但是边长为 2 的正方形包含 12 个苹果(如上图所示)。
周长为 2 * 4 = 8 。
示例 2:
输入:neededApples = 13
输出:16
示例 3:
输入:neededApples = 1000000000
输出:5040
提示:
题解
就挺那啥的。。。看推导公式的水平了
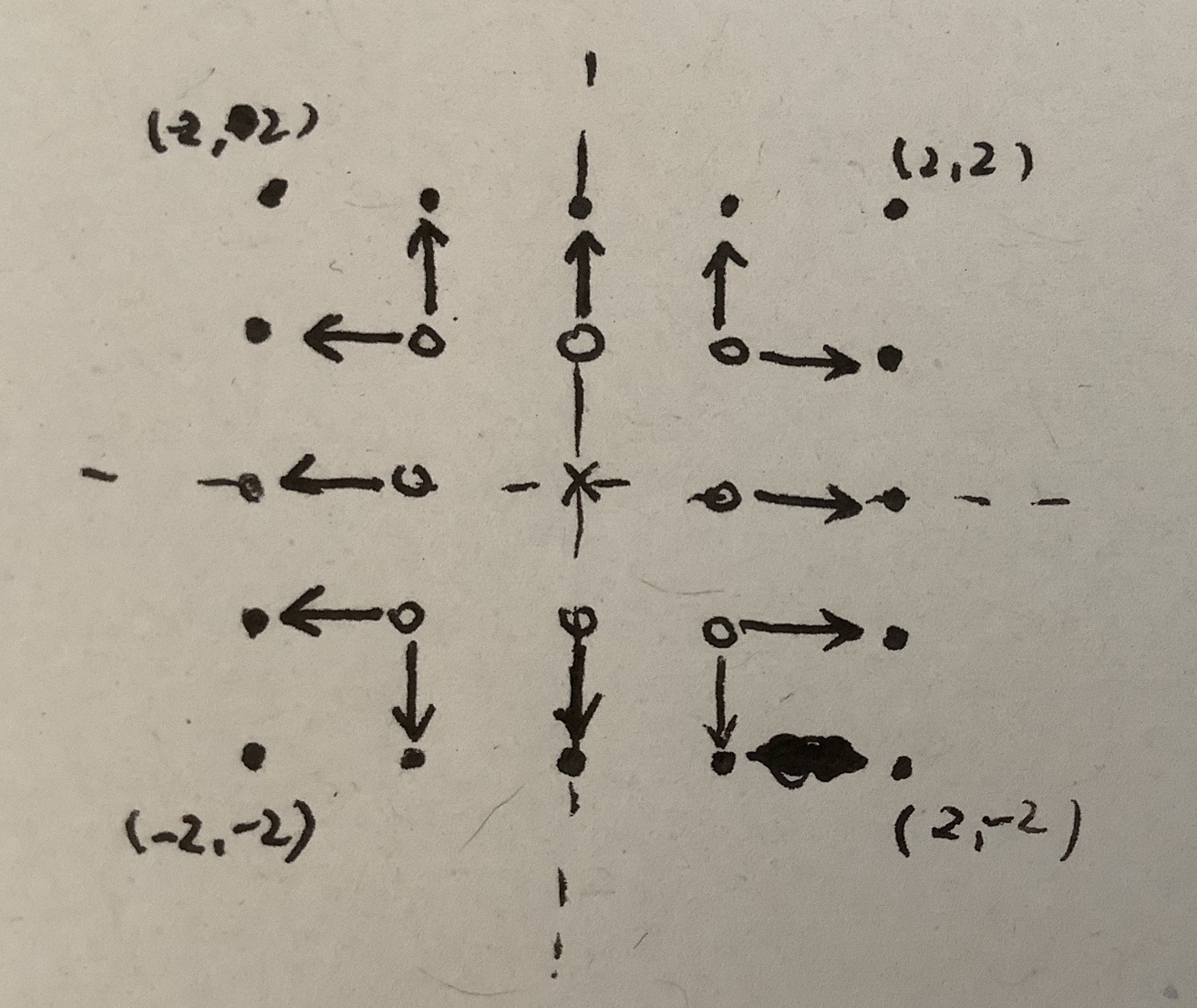
在这里我用cnt变量表示了各圈的苹果数量,用sum维护了当前总的苹果数量,edge表示了边长一半的长度,也就是正方形在一个象限内延伸的距离
每当edge增加一的时候,正方形外形就扩大一圈,我们可以认为是内圈各边上的各点向外平移一格的过程,期间内圈各点的坐标绝对值都经历了加一,我们要算出的就是内圈各边各点的个数,也就是每条边上面的点的个数 * 4(PS:内圈四个角要多重复计算一次,记得先补偿上去)
然后我们再把外圈的四个角补上,就完成了
代码如下:
1 | class Solution { |
看了眼答案题解,被降维打击了,标准做法,典中典啊。。。
如果正方形土地的右上角坐标为 (n, n),即边长为 2n,周长为 8n
对于坐标为 (x, y) 的树,它有 |x| + |y| 个苹果。因此,一块右上角坐标为 (n, n) 的正方形土地包含的苹果总数为:
由于 x 和 y 是对称的,因此:
你甚至可以用二分
1 | class Solution { |
T4 5833. 统计特殊子序列的数目
题目
特殊序列 是由 正整数 个 0 ,紧接着 正整数 个 1 ,最后 正整数 个 2 组成的序列。
比方说,[0,1,2] 和 [0,0,1,1,1,2] 是特殊序列。
相反,[2,1,0] ,[1] 和 [0,1,2,0] 就不是特殊序列。
给你一个数组 nums (仅 包含整数 0,1 和 2),请你返回 不同特殊子序列的数目 。由于答案可能很大,请你将它对 取余 后返回。
一个数组的 子序列 是从原数组中删除零个或者若干个元素后,剩下元素不改变顺序得到的序列。如果两个子序列的 下标集合 不同,那么这两个子序列是 不同的 。
示例 1:
输入:nums = [0,1,2,2]
输出:3
解释:特殊子序列为 [0,1,2,2],[0,1,2,2] 和 [0,1,2,2] 。
示例 2:
输入:nums = [2,2,0,0]
输出:0
解释:数组 [2,2,0,0] 中没有特殊子序列。
示例 3:
输入:nums = [0,1,2,0,1,2]
输出:7
解释:特殊子序列包括:[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
[0,1,2,0,1,2]
提示:
题解
经典老题,也许你还记得一年前LCP力扣杯秋季赛有这么一道题LCP 19. 秋叶收藏集
完全一模一样的做法,可以看做是一个DP,我们只需要从左向右遍历的过程中实时更新三种状态(即first状态 “0”, second状态“01”, third状态“012”)的种类数量即可
如果当前数字为0,我们知道first状态可以由first状态自身得来,即前面的全部first状态拼接一个新的“0”即可,所以first自加一次自己,但是还有“0”自身的情况没有考虑,所以再次自加1
如果当前数字是2,我们知道second状态可以由second状态叠加一个“1”得到,共有second种新情况,而单独的“1”是不能作为second状态的,所以我们这里没有自加一,故只自加second;此外second可以由之前first状态拼接“1”得到,所以自加所有的first情况数
如果当前的数字是3,同理,不再赘述
1 | class Solution { |
值得千提万提的是经典的取整,首先int类型在相加的过程中,由数据量我们知道有溢出的风险,所以中间过程所有变量都要采用long,此外long变量不断叠加的过程中也会发生溢出的可能,所以每次加法操作后要及时进行取余,防止long变量溢出变为负数。