跳表的简易实现（原理、代码）

简介

跳表（Skip List）是由 William Pugh 发明的一种查找数据结构，支持对数据的快速查找，插入和删除。跳表的期望空间复杂度为$O(n)$，跳表的查询，插入和删除操作的期望时间复杂度都为$O(log n)$。顾名思义，跳表是一种类似于链表的数据结构。

更加准确地说，跳表是对有序链表的改进。为方便讨论，后续所有有序链表默认为 升序 排序。

一个有序链表的查找操作，就是从头部开始逐个比较，直到当前节点的值大于或者等于目标节点的值。很明显，这个操作的复杂度是$O(n)$。

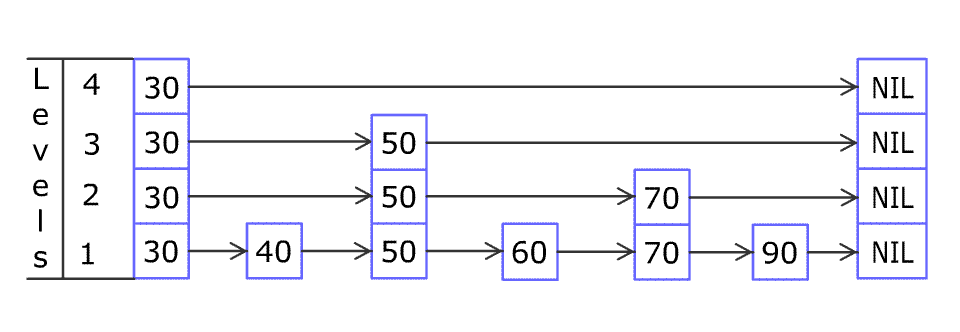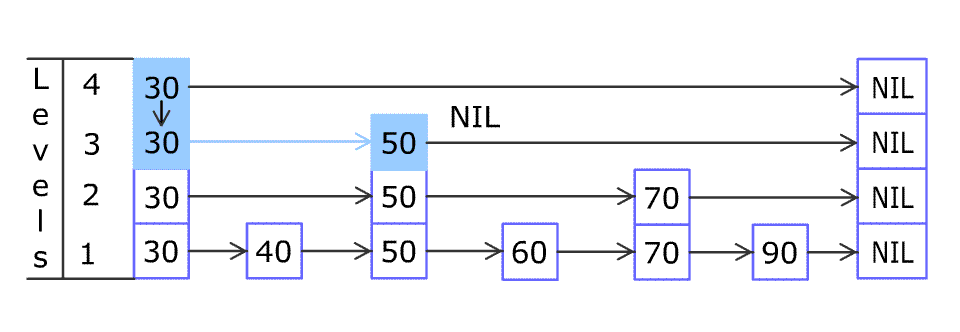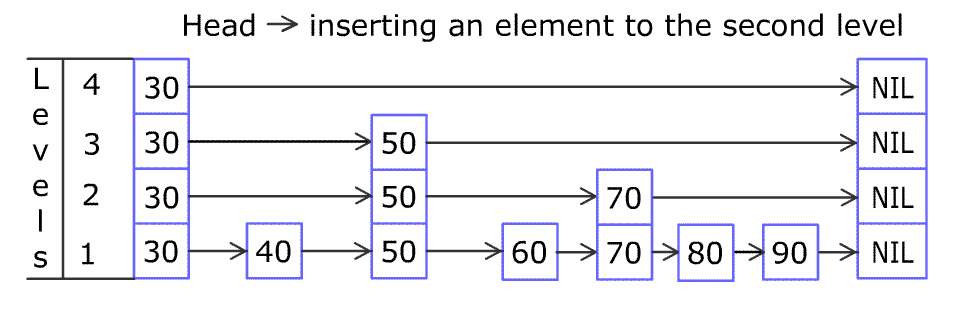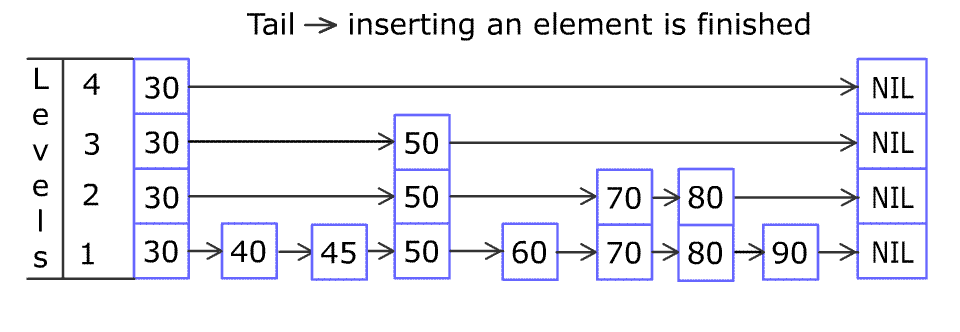
跳表在有序链表的基础上，引入了 分层 的概念。首先，跳表的每一层都是一个有序链表，特别地，最底层是初始的有序链表。每个位于第$i$层的节点有$p$的概率出现在第$i + 1$层， $p$为常数。

记在$n$个节点的跳表中，期望包含$\frac{1}{p}$个元素的层为第$L(n)$层，易得$L(n) = log_{\frac{1}{p}} n$。

在跳表中查找，就是从第$L(n)$层开始，水平地逐个比较直至当前节点的下一个节点大于等于目标节点，然后移动至下一层。重复这个过程直至到达第一层且无法继续进行操作。此时，若下一个节点是目标节点，则成功查找；反之，则元素不存在。这样一来，查找的过程中会跳过一些没有必要的比较，所以相比于有序链表的查询，跳表的查询更快。可以证明，跳表查询的平均复杂度为$O(log n)$。

对于一个节点而言，节点的最高层数为$i$的概率为$p^{i-1}(1-p)$。所以，跳表的期望层数为$\sum_{i>=1}^{}ip^{i-1}(1-p) = \frac{1}{1-p}$，且因为$p$为常数，所以跳表的 期望空间复杂度 为$O(n)$。

在最坏的情况下，每一层有序链表等于初始有序链表，即跳表的 最差空间复杂度 为$O(nlogn)$。

具体实现

我们可以配合leetcode例题辅助理解：1206. 设计跳表

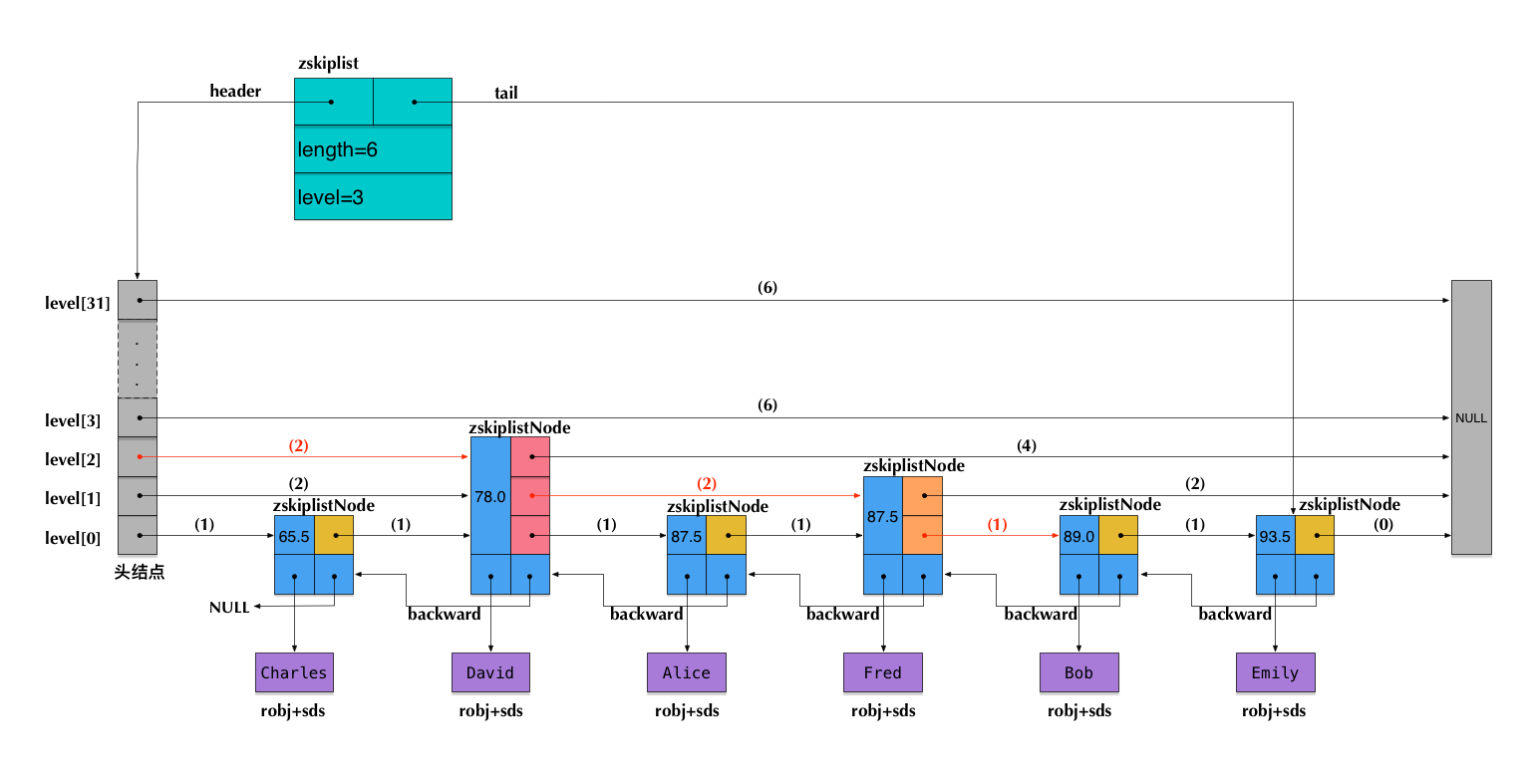
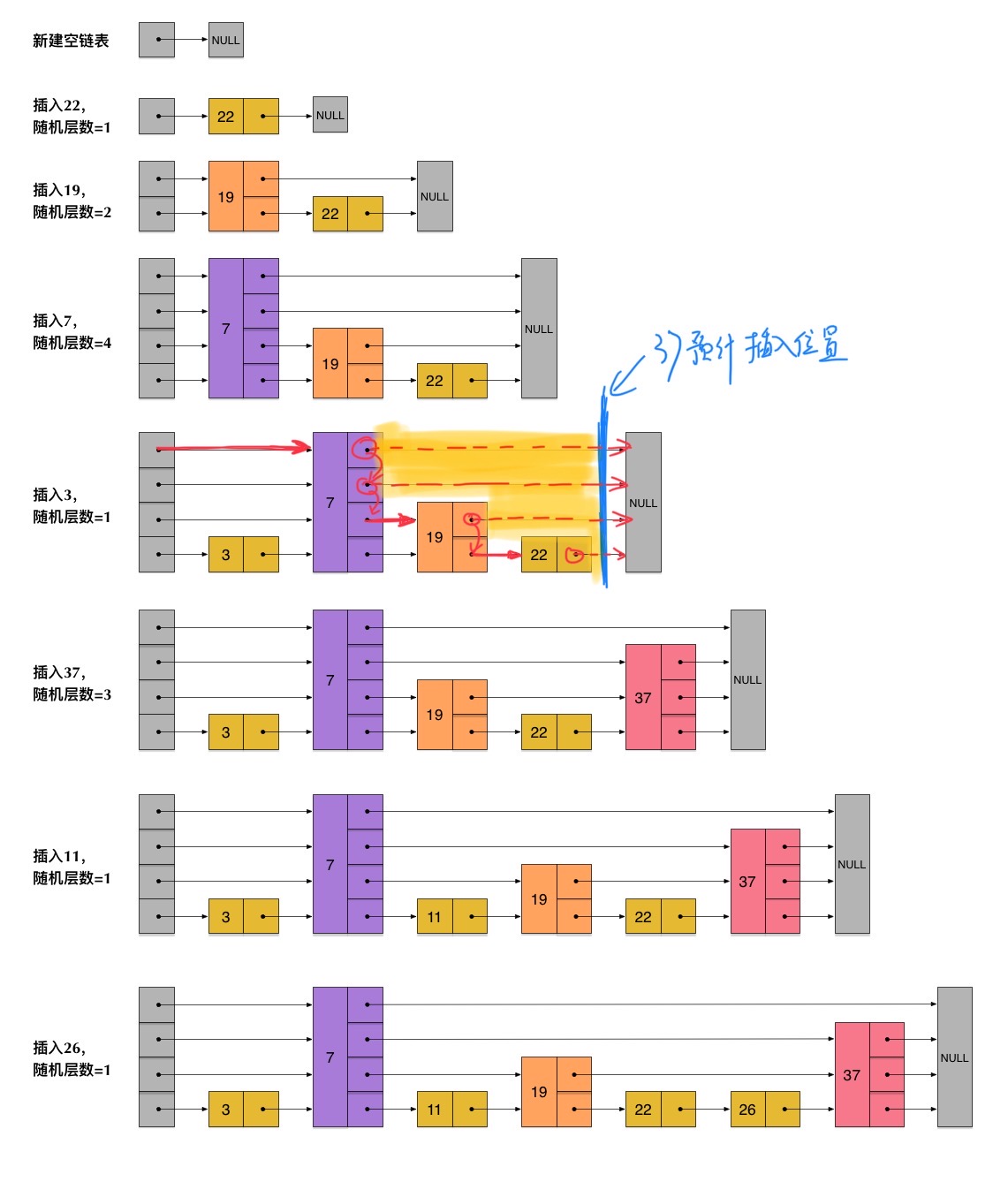
跳表中的各个元素都有自己的分层，具体层数由$p$概率和随机数进行决定，并且各层的密度自底向上依次递减。有点类似播放视频时的快进按钮，由于跳表内部各元素的排列都是有序的，上层节点跳转的速度最快是x16快进（打个比方），下层就是x8快进，以此类推，而最底层是x1正常速度前进。通过快进的方式，不断比较前进节点的值，我们可以在不回退的基础上不断对目标所在区间进行压缩，当当前层的区间粒度过大时，我们跳入下一层进行更细致的区间细分，这种方法相比纯粹暴力的$O(n)$遍历节省了时间。

确定节点的数据结构

由图中跳表最简单的实现逻辑，我们首先定义Node节点

我们规定Node[] fw，表示前进节点（forward），其中fw数组的大小情况由random()函数按照概率随机决定，但是针对例如head节点，例如其自身必须是最大深度，因此我们专门设置了一个可以指定fw数组大小的Node构造函数。

同时以int的方式存储val即节点的值，如下图：

private static final float SKIPLIST_P = 0.5f; //概率p
    private static final int MAX_LEVEL = 16; //最大层数，也就是head节点对应层数

    //单向链表
    class Node {
        int val;
        Node[] fw; //Node forward 前进节点

        public Node(int val) { //根据概率p随机确定节点层数
            this.val = val;
            fw = new Node[randomLevel()];
        }

        public Node(int val, int size) { //根据参数size直接指定节点层数
            this.val = val;
            fw = new Node[size];
        }

        private int randomLevel() { //随机函数，如果每次都有概率p进入下一层
            int level = 1;
            while (Math.random() < SKIPLIST_P && level < MAX_LEVEL - 1) level++;
            return level;
        }
    }

这是单向链表的简单实现情况，如果我们要实现双向链表，只需要在Node数据结构中加入Node bw即后退节点的指针即可，两者在查找的情形下实现方式都类似，但是在插入和删除中有所区别。需要指出的是bw节点指向的是最底层的节点。

private static final float SKIPLIST_P = 0.5f; //概率p
    private static final int MAX_LEVEL = 16; //最大层数，也就是head节点对应层数

    //双向链表
    class Node {
        int val;
        Node bw; //Node backward 后退节点
        Node[] fw; //Node forward 前进节点

        public Node(int val) { //根据概率p随机确定节点层数
            this.val = val;
            fw = new Node[randomLevel()];
        }

        public Node(int val, int size) { //根据size直接指定节点层数
            this.val = val;
            fw = new Node[size];
        }

        private int randomLevel() { //随机函数，如果每次都有概率p进入下一层
            int level = 1;
            while (Math.random() < SKIPLIST_P && level < MAX_LEVEL - 1) level++;
            return level;
        }
    }

当然啦，我们首先先忘记了初始化一个head节点：

class Skiplist {
        private static final float SKIPLIST_P = 0.5f;
        private static final int MAX_LEVEL = 16;
        Node head;

        class Node {
            //........见上
        }

        public Skiplist() {
            head = new Node(-1, MAX_LEVEL); //head节点直接初始化成最大高度
        }
    }

查找节点

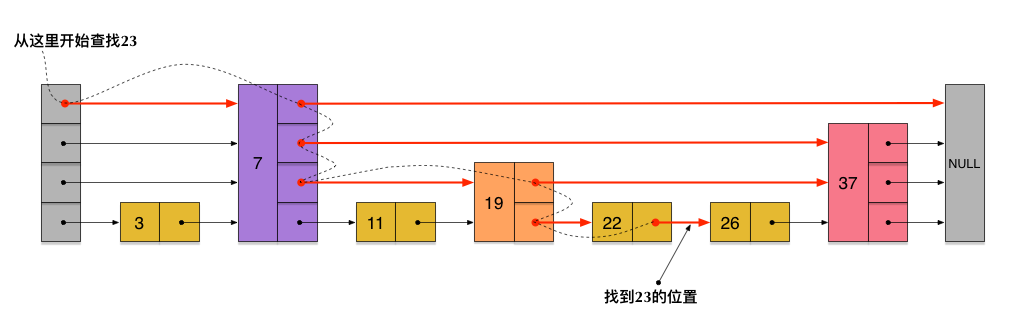
查找的过程，单向链表和双向链表的情况基本一致，因为跳表的特性，我们只需要比对当前节点的值、前进节点的值和目标值，再决定是否前进到前进节点还是进入下一层即可，如图：

这是我们在图中查找23的具体路径

非常容易理解，我们从head头节点的最顶层开始进行查找，这里的区间粒度最大，前进速度最快

• 如果前进节点的值仍然比目标值小（或者等于），那么我们就前进，因为这样可以快速的缩小范围也就是我们俗称的快进
  • 而当前进节点的值大于目标值（走到底了前面是null了也是一个道理），当前节点值小于目标值时，我们就知道这一层的快进速度太快啦，我们得到下一层慢慢走，继续细分区间范围
  • 而如果找不到目标值会怎么样呢，如果我们找不到目标值，很自然的，我们会一层一层的向下查找企图细分区间范围，直到到达最底层，这个时候如果仍然找不到节点我们就可以return false了。大家可以自己尝试一下。

代码实现呢倒也简单：

public boolean search(int target) {
     Node p = searchNode(target);
     return p.val == target;
 }

 private Node searchNode(int target) {
     if (isEmpty()) return head;
     Node p = head;
     for (int i = MAX_LEVEL - 1; i >= 0; i--) { //进入下一层
         while (p.fw[i] != null && p.fw[i].val <= target) { //节点前进
             p = p.fw[i];
         }
     }
     return p;
 }

 private boolean isEmpty() { //如果head最底层的前进都是空的，那表就是空的
     return head.fw[0] == null;
 }

这里为了偷懒就直接没有特判了hhh，所有的搜索节点searchNode()一律都走到了最底层，然后我们再拿目标值对照，如果匹配，那就是找到了，没有那就是没找到。

或者也可以在for循环里做如下修改：

while (p.fw[i] != null && p.fw[i].val <= target) {
    p = p.fw[i];
}
if (p.val == target) return p;

这样就可以在走到最底层前提前跳出了

插入节点

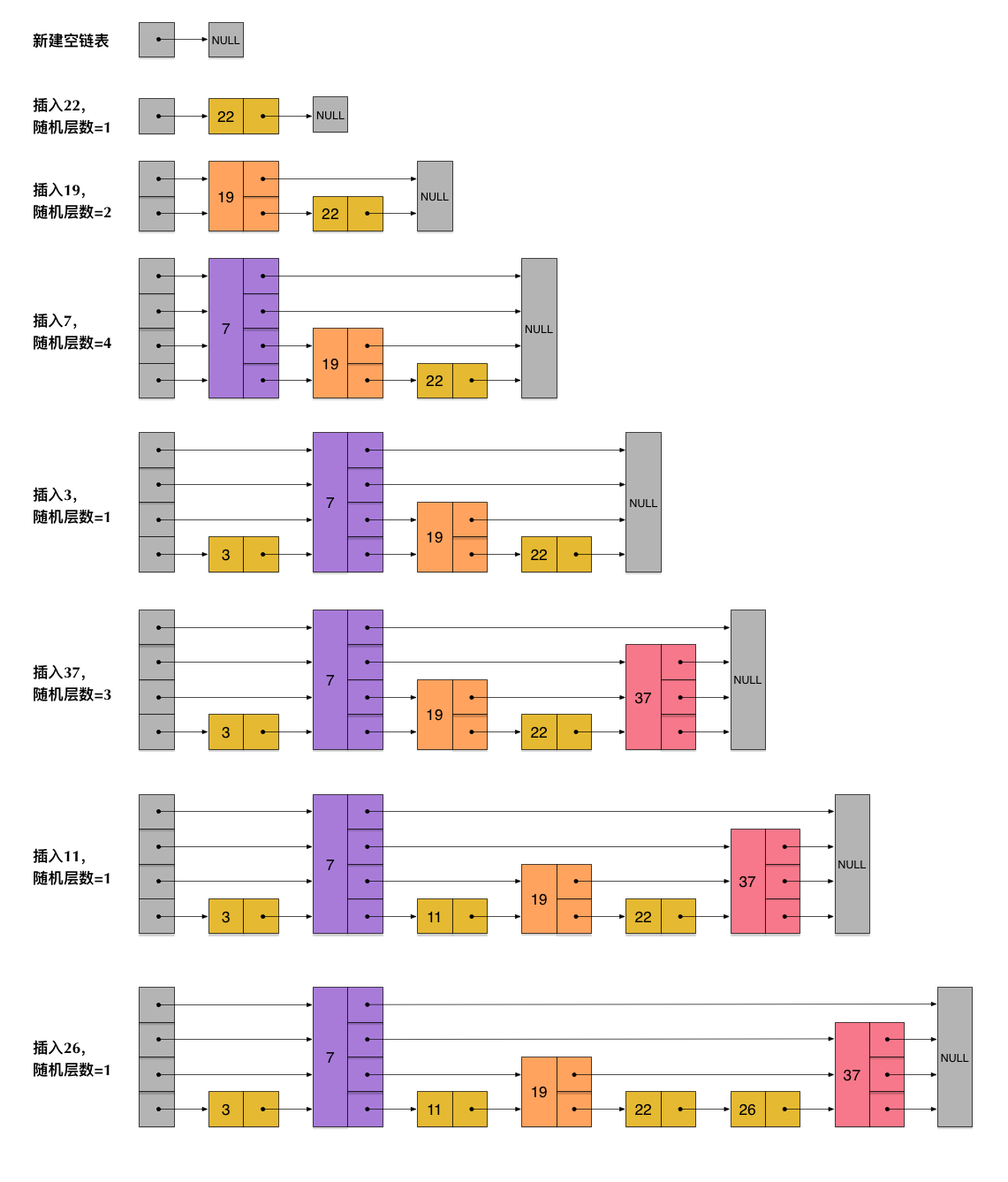
插入节点操作，想来好像蛮简单的hh，其实写起来蛮难受的，我们配合图片来理解一下：

我们以插入37的步骤为例：

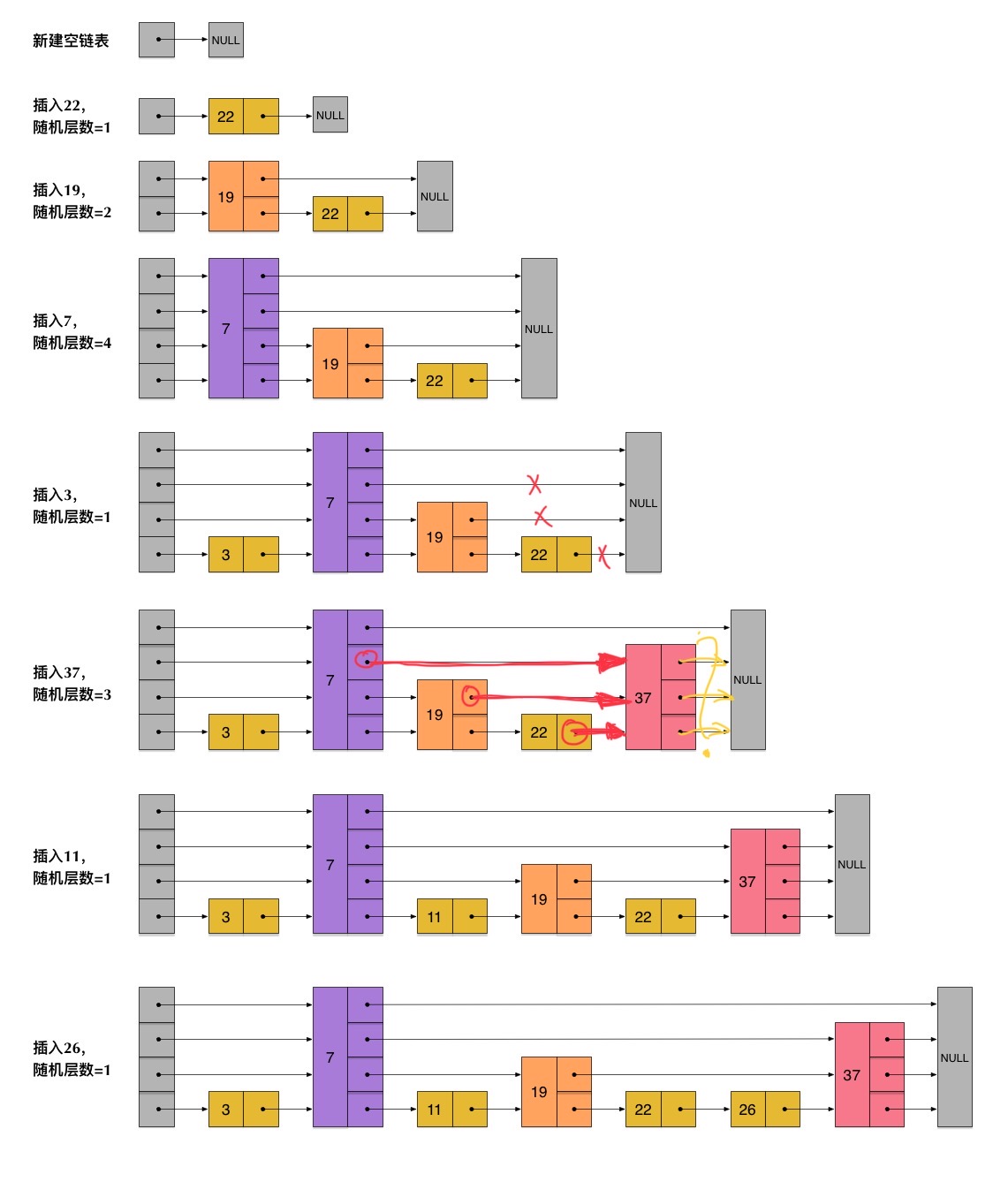
我们插入的节点可高可低，所以插入的节点我们即使通过searchNode()把它定位了大致确定放在哪个节点（也就是22后面）后了，还是会遇到蛮多讨厌的问题，像是这个37节点的高度可高可低，每层放眼向左看去可能会对应到不同的节点上去，就像上面图里面展示的一样，插入37时7，19，22的部分前进节点的指针都必须进行更改，此外我们还要将37的前进节点接上原7，19，22前进节点的指向，来确保后面不会断掉。

对于单向链表来说就很累了，因为我们不能回退，所以左视图的相关信息必须提前记录下，例如我们可以用一个数组Node[MAX_LEVEL]来表示。

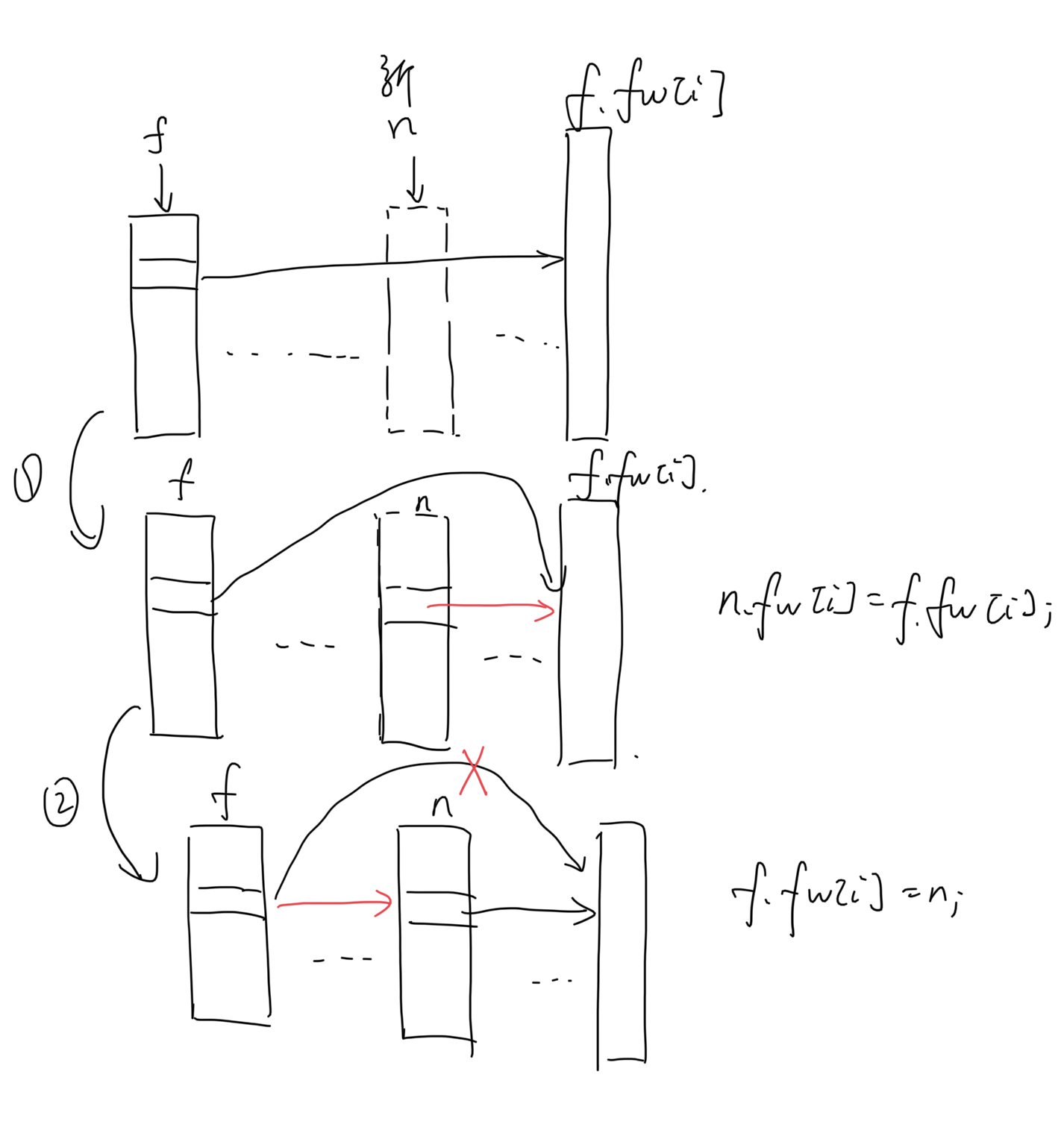
自顶层向下搜索target时，每次我们要向下进入下一层时，不知道细心的你有没有发现，这个节点就是本层target左视图暴露出来的节点。画个图表示一下，还是以37为例：

这样我们已经获得了37的完整左视图，不管37节点多高多低都无所谓了，我们的update数组中依次存储了22、19、7、7的节点指针（下标递增从0开始）

参考OI Wiki的写法，我实现了如下的Java代码：

public void add(int num) {
        Node[] update = new Node[MAX_LEVEL];
        Node p = head;
        for (int i = MAX_LEVEL - 1; i >= 0; i--) {
            //这段其实类似搜索，就是每次这层走到底的时候你得记录一下放到update数组里面
            while (p.fw[i] != null && p.fw[i].val <= num) {
                p = p.fw[i];
            }
            update[i] = p;
        }
        //获得了左视图各节点那就轻车熟路了
        //先创建新的节点，高度随机
        Node new_node = new Node(num);
        //先把新节点的前进节点接好，再把左视图节点前进指针指过来
        for (int i = 0; i < new_node.fw.length; i++) {
            new_node.fw[i] = update[i].fw[i];
            update[i].fw[i] = new_node;
        }
    }

这样是不是好理解多了

那换个角度，如果我们是双向链表呢？

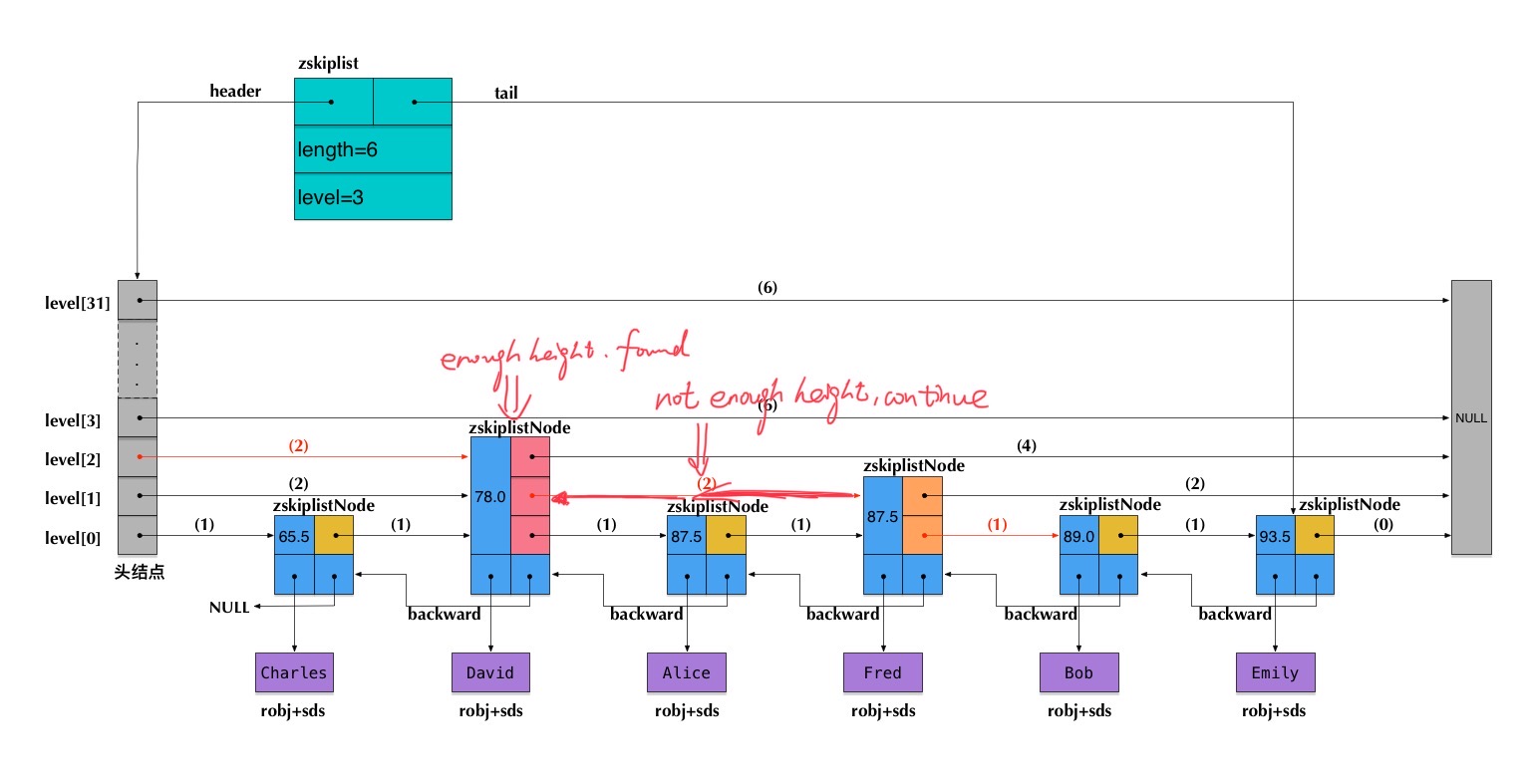
双向链表由于我们可以在最底层进行回退操作，这样的话可操作空间会更大，我们可以随意指定一层（例如第2层），然后使用bw指针向左遍历，第一个高度达到或者超过高度（第二层）的节点就是这层的左视图节点。

向左查找过程（以第二层为例）：

先贴个代码，繁琐的地方应该都在双向链表插入的逻辑上，可以多看几遍：

public void add(int num) {
        Node p = searchNode(num); //搜索num，新节点（在最底层）应当插在p的后面
        Node n = new Node(num); //创建随机高度新节点n
        n.bw = p; //先把新节点n的后退节点指向p
        for (int i = 0; i < n.fw.length; i++) { //第i层
            Node f = p;
            while (f.bw != null && f.fw.length < i + 1) {//向左看！直到节点高度满足要求
                f = f.bw;
            }
            //如果在最底层时，还要额外将该节点的前进节点的后退节点先指向新节点n
            if (i == 0 && f.fw[i] != null) f.fw[i].bw = n;
            //接下来是每层必须的操作
            n.fw[i] = f.fw[i]; //再将新节点n的前进节点指向该节点的前进节点
            f.fw[i] = n; //再将该节点的前进节点指向新节点n
        }
    }

删除节点

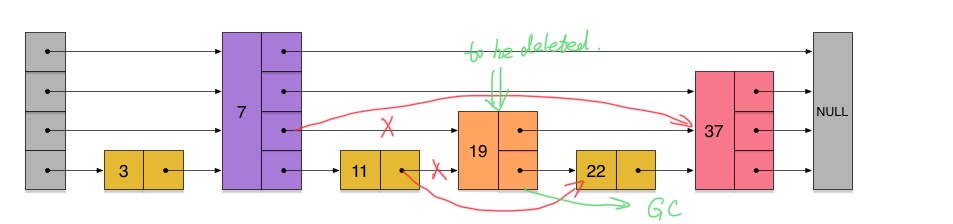
删除节点也是类似操作，画个图然后直接上代码了～逻辑和插入类似

对于单链表来说左视节点数组仍然是需要的，毕竟不能回退2333

简单来说就是一句话p.next = p.next.next;

public boolean erase(int num) {
        //例行判断，如果空就false
        if (isEmpty()) return false;
        Node[] update = new Node[MAX_LEVEL];
        Node p = head;
        for (int i = MAX_LEVEL - 1; i >= 0; i--) {
            //这段其实类似搜索，就是每次这层走到底的时候你得记录一下放到update数组里面，但是这次我们不能走到节点身上
            while (p.fw[i] != null && p.fw[i].val < target) {
                p = p.fw[i];
            }
            update[i] = p;
        }
        p = p.fw[0]; //p指向后一个位置（有可能是目标）
        if (p == null || p.val != num) return false; //不是就返回false
        for (int i = 0; i < p.fw.length; i++) {
            update[i].fw[i] = p.fw[i];
        }
        return true;
    }

对于双向链表来说，代码如下：

public boolean erase(int num) {
        if(isEmpty()) return false;
        Node p = searchNode(num);
        if(p.val != num) return false;
        for(int i = 0; i < p.fw.length; i++){
            Node f = p.bw;
            while(f.bw != null && f.fw.length < i + 1){
                f = f.bw;
            }
            if(i == 0 && f.fw[i].fw[i] != null) f.fw[i].fw[i].bw = f;
            f.fw[i] = f.fw[i].fw[i];
        }
        return true;
    }

总结

单向

class Skiplist {
    private static final float SKIPLIST_P = 0.5f;
    private static final int MAX_LEVEL = 16;

    Node head;

    class Node{
        int val;
        Node[] fw; //Node forward

        public Node(int val){
            this.val = val;
            fw = new Node[randomLevel()];
        }
        public Node(int val, int size){
            this.val = val;
            fw = new Node[size];
        }
        private int randomLevel(){
            int level = 1;
            while(Math.random() < SKIPLIST_P && level < MAX_LEVEL - 1) level++;
            return level;
        }
    }

    public Skiplist() {
        head = new Node(-1, MAX_LEVEL);
    }

    public boolean search(int target) {
        Node p = searchNode(target);
        return p.val == target;
    }

    public void add(int num){
        Node[] update = new Node[MAX_LEVEL];
        Node p = head;
        for(int i = MAX_LEVEL - 1; i >= 0; i--){
            //这段其实类似搜索，就是每次这层走到底的时候你得记录一下放到update数组里面
            while(p.fw[i] != null && p.fw[i].val <= num){
                p = p.fw[i];
            }
            update[i] = p;
        }
        //获得了左视图各节点那就轻车熟路了
        //先创建新的节点，高度随机
        Node new_node = new Node(num);
        //先把新节点的前进节点接好，再把左视图节点前进指针指过来
        for(int i = 0; i < new_node.fw.length; i++){
            new_node.fw[i] = update[i].fw[i];
            update[i].fw[i] = new_node;
        }
    }

    public boolean erase(int num){
        //例行判断，如果空就false
        if(isEmpty()) return false;
        Node[] update = new Node[MAX_LEVEL];
        Node p = head;
        for(int i = MAX_LEVEL - 1; i >= 0; i--){
            //这段其实类似搜索，就是每次这层走到底的时候你得记录一下放到update数组里面，但是这次我们不能走到节点身上
            while(p.fw[i] != null && p.fw[i].val < num){
                p = p.fw[i];
            }
            update[i] = p;
        }
        p = p.fw[0]; //p指向后一个位置（有可能是目标）
        if(p == null || p.val != num) return false; //不是就返回false
        for(int i = 0; i < p.fw.length; i++){
            update[i].fw[i] = p.fw[i];
        }
        return true;
    }

    private Node searchNode(int target){
        if(isEmpty()) return head;
        Node p = head;
        for(int i = MAX_LEVEL - 1; i >= 0; i--){
            while(p.fw[i] != null && p.fw[i].val <= target){
                p = p.fw[i];
            }
        }
        return p;
    }

    private boolean isEmpty(){
        return head.fw[0] == null;
    }
}

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist obj = new Skiplist();
 * boolean param_1 = obj.search(target);
 * obj.add(num);
 * boolean param_3 = obj.erase(num);
 */

双向

class Skiplist {
    private static final float SKIPLIST_P = 0.5f;
    private static final int MAX_LEVEL = 16;

    Node head;

    class Node{
        int val;
        Node bw; //Node backward
        Node[] fw; //Node forward

        public Node(int val){
            this.val = val;
            fw = new Node[randomLevel()];
        }
        public Node(int val, int size){
            this.val = val;
            fw = new Node[size];
        }
        private int randomLevel(){
            int level = 1;
            while(Math.random() < SKIPLIST_P && level < MAX_LEVEL - 1) level++;
            return level;
        }
    }

    public Skiplist() {
        head = new Node(-1, MAX_LEVEL);
    }

    public boolean search(int target) {
        Node p = searchNode(target);
        return p.val == target;
    }

    public void add(int num) {
        Node p = searchNode(num);
        Node n = new Node(num);
        n.bw = p;
        for(int i = 0; i < n.fw.length; i++){
            Node f = p;
            while(f.bw != null && f.fw.length < i + 1){
                f = f.bw;
            }
            if(i == 0 && f.fw[i] != null) f.fw[i].bw = n;
            n.fw[i] = f.fw[i];
            f.fw[i] = n;
        }
    }

    public boolean erase(int num) {
        if(isEmpty()) return false;
        Node p = searchNode(num);
        if(p.val != num) return false;
        for(int i = 0; i < p.fw.length; i++){
            Node f = p.bw;
            while(f.bw != null && f.fw.length < i + 1){
                f = f.bw;
            }
            if(i == 0 && f.fw[i].fw[i] != null) f.fw[i].fw[i].bw = f;
            f.fw[i] = f.fw[i].fw[i];
        }
        return true;
    }

    private Node searchNode(int target){
        if(isEmpty()) return head;
        Node p = head;
        for(int i = MAX_LEVEL - 1; i >= 0; i--){
            while(p.fw[i] != null && p.fw[i].val <= target){
                p = p.fw[i];
            }
        }
        return p;
    }

    private boolean isEmpty(){
        return head.fw[0] == null;
    }
}

/**
 * Your Skiplist object will be instantiated and called as such:
 * Skiplist obj = new Skiplist();
 * boolean param_1 = obj.search(target);
 * obj.add(num);
 * boolean param_3 = obj.erase(num);
 */