关于学习资源和视频等问题可以参考第一次写的Data Lab 开头中提及的相关问题。
上次的Architecture Lab做的也是难受,不过主要的时间应该是耗在看书上了,每天晚上零零碎碎花了点时间一点一点啃掉的… 由于我脑回路新奇,经常读不懂或者曲解作者意思,每次还得反复读来确认,不管怎么说,最后完全理解的时候成就感还是非常强的。
前段时间还花了小半天时间把服务器从Tencent Cloud HK 迁移到 AWS Tokyo,一是确实不太满意腾讯给的小水管带宽,我的frp内网穿透速度根本拉不起来;二是腾讯云上用着的CentOS 8貌似有亿点点老了,本着长痛不如短痛的想法,我还是把它给换了,迁移了博客、短链接、订阅转换等服务blabla…
回到正题,这次的Cache Lab貌似也不简单… Part A要求的程序要从零写起,直接开幕雷击…
本次实验将帮助我们更好的理解Cache缓存对我们的C语言程序产生的影响。实验共分为两个部分,在第一个部分中,我们需要写一段简单的C语言程序(大致控制在200~300行)来模拟Cache缓存的行为,而在第二个部分中,我们将优化一个小型的矩阵转置方法,使得尽可能少的触发缓存未命中。
准备
对应课程
这次的Cache Lab作业,如果是自学,在B站课程 中,应该大致需要完成P11~P12的学习,大致了解存储设备的金字塔模型,以及Cache高速缓存的存储器组织结构。
课程文件
相关的作业可以在CMU的官网上找到:
Lab Assignments
在Cache Lab一栏里面,我们可以查看相关文件,例如:
下载后并解压的文件如图所示:
使用环境
继续使用Arch Linux,系统版本和GCC版本如下:
使用建议
我们需要进行修改的文件只有csim.c和trans.c这两个,修改完之后执行:
编译即可。
题目
Part A
了解valgrind工具箱
valgrind 是一个提供了一些 debug 和优化的工具的工具箱,可以使得你的程序减少内存泄漏或者错误访问。
有兴趣的可以先安装一下,不过在Part A貌似用不着:
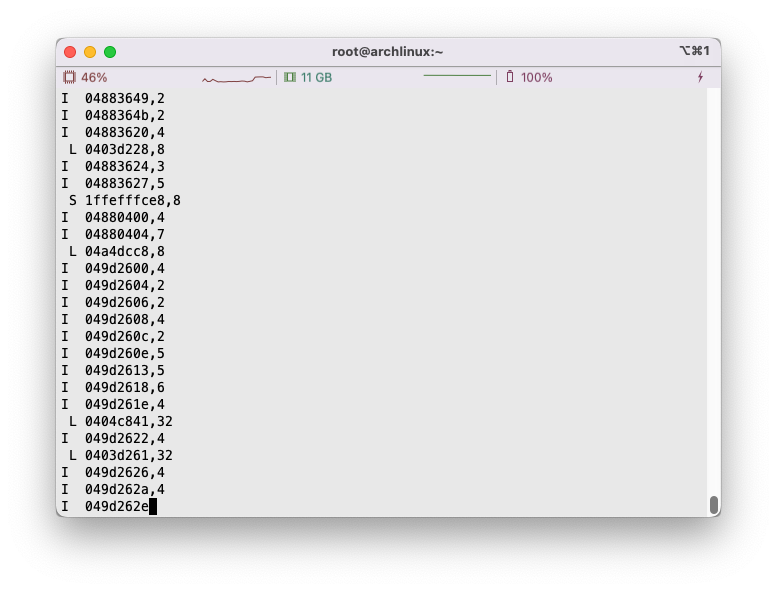
我们通过给定一个命令,就可以让 valgrind 进行内存使用的分析,例如我们如果想研究ls -l运行过程中的内存活动,我们可以输入:
1 valgrind --log-fd=1 --tool=lackey -v --trace-mem=yes ls -l
将内存使用的情况按照顺序打印在stdout标准输出中,如下图:
关于valgrind的相关文档可以参考:
其中,我们前往valgrind的官网:User Manual
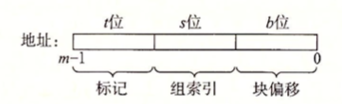
注意到,valgrind的内存分析格式例如:
1 2 3 4 I 0400d7d4,8 M 0421c7f0,4 L 04f6b868,8 S 7ff0005c8,8
每一行表示的内存访问格式形如:
1 [space]operation address,size
operation一栏表示了内存访问的类型,例如I表示指令加载(Instruction Load),L表示数据加载(Data Load),S表示数据存储(Data Store),而M表示数据修改(Data Modify),相当于一次加载和一次缓存。在I指令前不会有空格,而在M, L和S指令前均有一个空格。address一栏是一个表示64位的16进制地址,表示内存地址。size则表示本次本次内存操作的字节数大小。
题目描述中,在目录traces下,就存在着若干这样的文件,例如yi.trace:
1 2 3 4 5 6 7 L 10,1 M 20,1 L 22,1 S 18,1 L 110,1 L 210,1 M 12,1
实现目标
题目需要我们自己几乎从零开始编写csim.c文件,使得通过编译后csim实现的功能与文件夹内已经存在的可执行文件csim-ref功能一致。
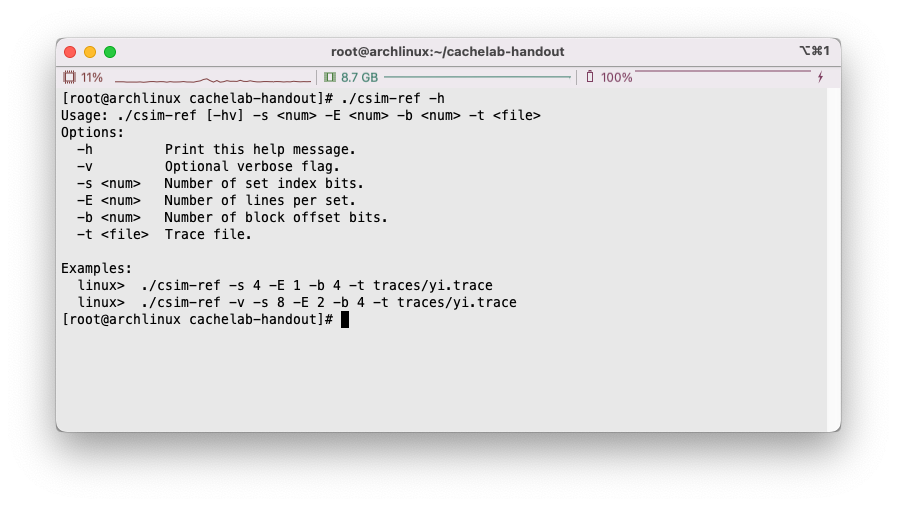
而csim-ref所实现的功能就是根据trace文件的内容,和给定的高速缓存结构参数,分析出高速缓存的逐步操作。其参数对应描述如下:
1 2 3 4 5 6 7 Usage: ./csim-ref [-hv] -s <s> -E <E> -b <b> -t <tracefile> • -h: Optional help flag that prints usage info • -v: Optional verbose flag that displays trace info • -s <s>: Number of set index bits (S = 2^s is the number of sets) • -E <E>: Associativity (number of lines per set) • -b <b>: Number of block bits (B = 2^b is the block size) • -t <tracefile>: Name of the valgrind trace to replay
值得注意的是,该缓存模型使用的是LRU淘汰算法,优先淘汰最久没有使用的缓存。
示例如下,如果我们给定共16个高速缓存组,每组1个高速缓存行, 每行由16字节的缓存块构成:
1 2 linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace hits:4 misses:5 evictions:3
显示为命中4次,未命中5次,淘汰3次。
加入-v参数,还可观察到更多细节:
1 2 3 4 5 6 7 8 9 linux> ./csim-ref -v -s 4 -E 1 -b 4 -t traces/yi.trace L 10,1 miss M 20,1 miss hit L 22,1 hit S 18,1 hit L 110,1 miss eviction L 210,1 miss eviction M 12,1 miss eviction hit hits:4 misses:5 evictions:3
PDF中明确指出了,我们本次实验只关心数据缓存的表现,因此对于I相关的指令,一律直接忽视(可以合理利用I开头指令没有空格来进行区分)
此外,PDF中还指出了,假设所有的内存是全部对齐的,我们尝试访问的数据也不会跨越block块。因此根据这点,我们可以直接忽略测试数据中的数据大小。
P.S.
在这里,我们尝试对刚才的结果进行一下理解,为啥是命中4次,未命中5次,淘汰3次。
L 10, 1时,0x10看作00...000010000,表示为第1个高速缓存组,由于内部的缓存行有效位无效,因此直接未命中missM 20, 1时,0x20看作00...000100000,表示为第2个高速缓存组, M表示修改,即两次连续访问。因此先miss,后hitL 22, 1时,0x22看作00...000100010,表示为第2个高速缓存组,标记对应M 20, 1时的缓存,因此缓存命中hitS 18, 1时,0x18看作00...000011000,表示为第1个高速缓存组,标记对应L 10, 1时的缓存,因此缓存命中hitL 110, 1时,0x110看作00...100010000,表示第1个高速缓存组,但是标记为1,与缓存中的0不符,因此未命中miss,并将这一行进行驱逐L 210, 1时,0x210看作00..1000010000,表示第1个高速缓存组,但是标记2,与缓存中的1不符,因此未命中miss,并将这一行进行驱逐M 12, 1时,0x12看作00...000010010,表示为第1个高速缓存组,但是标记为0,与缓存中2不符,由于是M表示修改,因此先miss并eviction,后hit
P.S.
这里可以先提一嘴,LRU是在哪里被使用的,因为上方的例子由于每个高速缓存组内部的缓存行只有一行而没法得到很好的体现。
当我们得到一个地址的时候,我们首先根据其二进制编码确定他应该查询哪个缓存组,而在缓存组内部我们应当首先逐个的查询是否有和标记为匹配的缓存行,如果有那么我们就认定为命中hit。而如果没有命中miss,且在缓存组中仍然有缓存行的有效位为0,也就是处于空闲的状态,我们就直接讲从下级存储单元获取的内容填入当前的空闲缓存行中。而如果既没有命中,缓存组内部也没有多余的缓存行时,我们就考虑先驱逐最久未使用的缓存行,这就是LRU的实现方式 。关于LRU的实现方式,可以参考LRU 算法小结 。
代码实现
数据结构
由于储存器的参数都是通过-s, -E, -b传入的,因此我们需要动态申请数据结构。
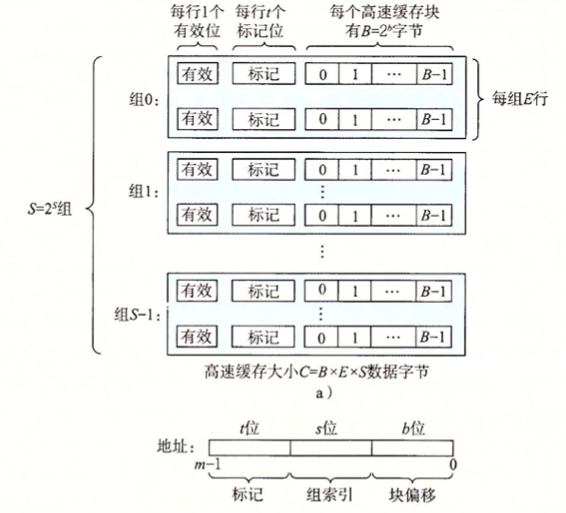
我们根据Cache的组织结构,模拟出一个类似的组织结构:
1 2 3 4 5 6 7 8 9 10 11 12 13 typedef struct { bool valid; unsigned long long tag; int timeStamp; } cacheLine; typedef struct { cacheLine* lines; } cacheSet; typedef struct { cacheSet* sets; } cache;
可以看到,缓存由S个高速缓存组组成,每个高速缓存组内由E个缓存行构成。
缓存行内部由有效位valid,标志位tag和B字节的高速缓存块组成。但是由于模拟的关系,我们暂时用不着缓存块,因此,不放入数据结构中。此外,由于要实现LRU算法,我们需要对各缓存行留下额外的空间保存最近更新的时间戳timeStamp,以便到时确定应该驱逐哪一条缓存行。
使用时间戳算是比较简单且浅显易懂的实现方式了,用HashMap和双向链表我用C语言是真的写不动了:(
打印帮助提示
当输入-h指令时,或者当输入参数不正确的时候,我们需要打印使用提示。如下:
这个很好解决,如下即可:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void printUsage () { printf ( "Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>\n" "Options:\n" " -h Print this help message.\n" " -v Optional verbose flag.\n" " -s <num> Number of set index bits.\n" " -E <num> Number of lines per set.\n" " -b <num> Number of block offset bits.\n" " -t <file> Trace file.\n\n" "Examples:\n" " linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n" " linux> ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n" ); }
获取输入参数
每次运行时,都会从终端传入-s, -E, -b等相关参数,因此我们要正确的获取到相关参数,如有异常还需要进一步做出异常判断。在这里我们调用标准库中的getopt函数来解决问题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 void getParam (int argc, char * argv[]) { int opt; while (-1 != (opt = getopt(argc, argv, "hvs:E:b:t:" ))) { switch (opt) { case 'h' : h = true ; break ; case 'v' : v = true ; break ; case 's' : s = atoi(optarg); break ; case 'E' : E = atoi(optarg); break ; case 'b' : b = atoi(optarg); break ; case 't' : t = (char *)calloc (1000 , sizeof (char )); strcpy (t, optarg); break ; default : printUsage(); break ; } } if (h) { printUsage(); exit (0 ); } if (s <= 0 || E <= 0 || b <= 0 || t == NULL ) { printf ("%s: Missing required command line argument\n" , argv[0 ]); printUsage(); exit (-1 ); } }
初始化缓存结构
根据刚才传入的各个参数,可以准备开始初始化缓存结构了,我们有:
1 2 3 4 5 6 7 8 9 10 cache* initCache (int s, int E) { int S = 1 << s; cache* c = (cache*)calloc (1 , sizeof (cache)); cacheSet* setArr = (cacheSet*)calloc (S, sizeof (cacheSet)); c->sets = setArr; for (int i = 0 ; i < S; i++) { (setArr + i)->lines = (cacheLine*)calloc (E, sizeof (cacheLine)); } return c; }
释放申请空间
当程序结束时,我们需要手动释放我们通过calloc申请的内存,内存包括缓存的数据结构c和参数t字符串申请的空间:
1 2 3 4 5 6 7 8 9 10 void releaseMem (cache* c, char * t) { int S = 1 << s; for (int i = 0 ; i < S; i++) { cacheSet* set = c->sets + i; free (set ->lines); } free (c->sets); free (c); free (t); }
读取文件并处理
接下来我们需要打开对应路径对trace文件,对内部的内容进行读取和分析。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 void processFile (char * path, cache* c) { FILE* fp = fopen(path, "r" ); if (fp == NULL ) { printf ("%s: No such file or directory\n" , path); exit (-1 ); } char op; unsigned long long addr; int size; char strLine[1024 ]; while (fgets(strLine, sizeof (strLine), fp)) { if (strLine[0 ] == 'I' ) continue ; if (sscanf (strLine, " %c %llX,%d" , &op, &addr, &size) < 3 ) { printf ("%s: Invalid Argument %s" , path, strLine); exit (-1 ); } if (v) printf ("%c %llX,%d " , op, addr, size); accessCache(op, addr, c); } fclose(fp); }
访问缓存
根据给出的地址,我们通过简单的位运算很方便的能够得出映射到的具体是哪一个高速缓存块,并且我们可以计算出对应的标记位。
详情见:
1 2 3 4 5 6 void accessCache (char op, unsigned long long addr, cache* c) { int matchTag = addr >> (b + s); int matchSetAddr = (addr >> b) & ((1 << s) - 1 ); cacheSet* set = c->sets + matchSetAddr; accessCacheSet(matchTag, op, set ); }
访问缓存块
我们需要处理的操作共有三种,分别是L, M, S,其中L和S分别代表数据加载和数据存储,需要访问地址一次,而M操作,可以看作两种操作的结合,需要访问地址两次。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void accessCacheSet (unsigned long long matchTag, char op, cacheSet* set ) { switch (op) { case 'L' : lruUpdateSet(matchTag, set , 1 ); break ; case 'M' : lruUpdateSet(matchTag, set , 2 ); break ; case 'S' : lruUpdateSet(matchTag, set , 1 ); break ; default : printf ("Invalid op %c\n" , op); exit (-1 ); } }
LRU访问地址细节
接下来这一部分应该是整段代码的重中之重,因为他涉及了LRU算法的实现。
我们简单的梳理一下各种操作可能的情形,由于M操作第二次是操作的同一个地址,因此必为hit。而M, L和S第一次操作就有如下可能性:
Hit,标志位和缓存组内部某一有效行对应,命中
Miss,标志位没有和任意一行有效行对应,未命中
但是,缓存组内部存在空闲未使用的无效行,更新缓存时可直接将其填入
Evict,或者,没有空闲的缓存行,必须挑选一条最久未使用的缓存行将其驱逐,将新的数据更新进去
综上:L和S操作可能会发生:hit, miss和miss eviction。M操作可能会发生hit hit, miss hit, miss eviction hit。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 void lruUpdateSet (unsigned long long matchTag, cacheSet* set , int times) { int isMiss = 0 , isHit = 0 , isEvict = 0 ; for (int k = 0 ; k < times; k++) { for (int i = 0 ; i < E; i++) { cacheLine* line = set ->lines + i; if (line->valid && matchTag == line->tag) { isHit++; if (v) printf ("%s " , "hit " ); line->timeStamp = curTimeStamp++; break ; } } if (isHit) continue ; isMiss++; if (v) printf ("%s" , "miss " ); bool isFilled = false ; for (int i = 0 ; i < E; i++) { cacheLine* line = set ->lines + i; if (!line->valid) { line->tag = matchTag; line->valid = true ; line->timeStamp = curTimeStamp++; isFilled = true ; break ; } } if (isFilled) continue ; isEvict++; if (v) printf ("%s" , "eviction " ); cacheLine* oldestLine; int minStamp = 0x7fffffff ; for (int i = 0 ; i < E; i++) { cacheLine* line = set ->lines + i; if (minStamp > line->timeStamp) { minStamp = line->timeStamp; oldestLine = line; } } oldestLine->tag = matchTag; oldestLine->timeStamp = curTimeStamp++; } if (v) printf ("\n" ); hit += isHit; miss += isMiss; eviction += isEvict; }
main函数实现
main函数如下即可,较为简单:
1 2 3 4 5 6 7 8 int main (int argc, char * argv[]) { getParam(argc, argv); cache* c = initCache(s, E); processFile(t, c); releaseMem(c, t); printSummary(hit, miss, eviction); return 0 ; }
其中,最后的printSummary方法,就是简单的打印总计数,详情见文件夹下的cachelab.c:
1 2 3 4 5 6 7 void printSummary (int hits, int misses, int evictions) { printf ("hits:%d misses:%d evictions:%d\n" , hits, misses, evictions); FILE* output_fp = fopen(".csim_results" , "w" ); assert(output_fp); fprintf (output_fp, "%d %d %d\n" , hits, misses, evictions); fclose(output_fp); }
总结&测试
写的实在是太丑陋了:(
万年不写C了,大学进去的时候就没学好,差点要老命。
最后的代码成型为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 #include <getopt.h> #include <stdbool.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include "cachelab.h" typedef struct { bool valid; unsigned long long tag; int timeStamp; } cacheLine; typedef struct { cacheLine* lines; } cacheSet; typedef struct { cacheSet* sets; } cache; int s, E, b;bool h, v;char * t;int miss, hit, eviction;int curTimeStamp;void printUsage () ;void getParam (int argc, char * argv[]) ;cache* initCache (int s, int E) ; void releaseMem (cache* c, char * t) ;void processFile (char * path, cache* c) ;void accessCache (char op, unsigned long long addr, cache* c) ;void accessCacheSet (unsigned long long matchTag, char op, cacheSet* set ) ;void lruUpdateSet (unsigned long long matchTag, cacheSet* set , int times) ;void printUsage () { printf ( "Usage: ./csim-ref [-hv] -s <num> -E <num> -b <num> -t <file>\n" "Options:\n" " -h Print this help message.\n" " -v Optional verbose flag.\n" " -s <num> Number of set index bits.\n" " -E <num> Number of lines per set.\n" " -b <num> Number of block offset bits.\n" " -t <file> Trace file.\n\n" "Examples:\n" " linux> ./csim-ref -s 4 -E 1 -b 4 -t traces/yi.trace\n" " linux> ./csim-ref -v -s 8 -E 2 -b 4 -t traces/yi.trace\n" ); } void getParam (int argc, char * argv[]) { int opt; while (-1 != (opt = getopt(argc, argv, "hvs:E:b:t:" ))) { switch (opt) { case 'h' : h = true ; break ; case 'v' : v = true ; break ; case 's' : s = atoi(optarg); break ; case 'E' : E = atoi(optarg); break ; case 'b' : b = atoi(optarg); break ; case 't' : t = (char *)calloc (1000 , sizeof (char )); strcpy (t, optarg); break ; default : printUsage(); break ; } } if (h) { printUsage(); exit (0 ); } if (s <= 0 || E <= 0 || b <= 0 || t == NULL ) { printf ("%s: Missing required command line argument\n" , argv[0 ]); printUsage(); exit (-1 ); } } cache* initCache (int s, int E) { int S = 1 << s; cache* c = (cache*)calloc (1 , sizeof (cache)); cacheSet* setArr = (cacheSet*)calloc (S, sizeof (cacheSet)); c->sets = setArr; for (int i = 0 ; i < S; i++) { (setArr + i)->lines = (cacheLine*)calloc (E, sizeof (cacheLine)); } return c; } void releaseMem (cache* c, char * t) { int S = 1 << s; for (int i = 0 ; i < S; i++) { cacheSet* set = c->sets + i; free (set ->lines); } free (c->sets); free (c); free (t); } void processFile (char * path, cache* c) { FILE* fp = fopen(path, "r" ); if (fp == NULL ) { printf ("%s: No such file or directory\n" , path); exit (-1 ); } char op; unsigned long long addr; int size; char strLine[1024 ]; while (fgets(strLine, sizeof (strLine), fp)) { if (strLine[0 ] == 'I' ) continue ; if (sscanf (strLine, " %c %llX,%d" , &op, &addr, &size) < 3 ) { printf ("%s: Invalid Argument %s" , path, strLine); exit (-1 ); } if (v) printf ("%c %llX,%d " , op, addr, size); accessCache(op, addr, c); } fclose(fp); } void accessCache (char op, unsigned long long addr, cache* c) { int matchTag = addr >> (b + s); int matchSetAddr = (addr >> b) & ((1 << s) - 1 ); cacheSet* set = c->sets + matchSetAddr; accessCacheSet(matchTag, op, set ); } void accessCacheSet (unsigned long long matchTag, char op, cacheSet* set ) { switch (op) { case 'L' : lruUpdateSet(matchTag, set , 1 ); break ; case 'M' : lruUpdateSet(matchTag, set , 2 ); break ; case 'S' : lruUpdateSet(matchTag, set , 1 ); break ; default : printf ("Invalid op %c\n" , op); exit (-1 ); } } void lruUpdateSet (unsigned long long matchTag, cacheSet* set , int times) { int isMiss = 0 , isHit = 0 , isEvict = 0 ; for (int k = 0 ; k < times; k++) { for (int i = 0 ; i < E; i++) { cacheLine* line = set ->lines + i; if (line->valid && matchTag == line->tag) { isHit++; if (v) printf ("%s " , "hit " ); line->timeStamp = curTimeStamp++; break ; } } if (isHit) continue ; isMiss++; if (v) printf ("%s" , "miss " ); bool isFilled = false ; for (int i = 0 ; i < E; i++) { cacheLine* line = set ->lines + i; if (!line->valid) { line->tag = matchTag; line->valid = true ; line->timeStamp = curTimeStamp++; isFilled = true ; break ; } } if (isFilled) continue ; isEvict++; if (v) printf ("%s" , "eviction " ); cacheLine* oldestLine; int minStamp = 0x7fffffff ; for (int i = 0 ; i < E; i++) { cacheLine* line = set ->lines + i; if (minStamp > line->timeStamp) { minStamp = line->timeStamp; oldestLine = line; } } oldestLine->tag = matchTag; oldestLine->timeStamp = curTimeStamp++; } if (v) printf ("\n" ); hit += isHit; miss += isMiss; eviction += isEvict; } int main (int argc, char * argv[]) { getParam(argc, argv); cache* c = initCache(s, E); processFile(t, c); releaseMem(c, t); printSummary(hit, miss, eviction); return 0 ; }
我们以刚才分析的trace数据为例,效果和csim-ref完全相同:
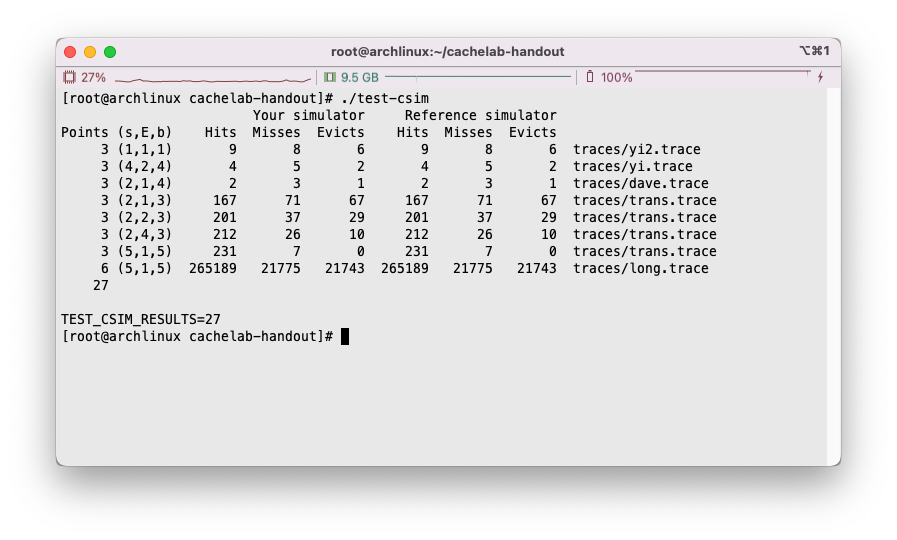
运行test-csim,将我们写出的程序和csim-ref进行比对,完全一致,得满分:
Part B
实现目标
在此部分中,题目要求我们实现一个矩阵的转置方法,将一个N × M N \times M N × M A,转置后输出到M × N M \times N M × N B空间中去。
在PDF中,指定了缓存的大小和测试样例大小,要求我们使用参数-s 5 -E 1 -b 5,也就是说缓存共有32个高速缓存组,每个缓存组中只有1个高速缓存行,每行中的缓存块大小为32字节。
给定的测试矩阵大小有三种,分别为(以下参数M在前,N在后):
32 × 32 32 \times 32 32 × 32 64 × 64 64 \times 64 64 × 64 61 × 67 61 \times 67 61 × 67
注意事项
最多使用 12 个 int 类型的本地变量。
不能修改 A 矩阵的内容,B 矩阵可随意修改。
不能用 malloc 类函数申请内存。
矩阵A和矩阵B的内存分布是连续的。
P.S.
参考了很多博客,感觉有块部分讲的不是很清楚,那就是我们给定的缓存非常的小,如果设计访问两个矩阵的内存空间,必然会导致映射到的缓存组发生重合,那么是怎么样的一种映射关系呢?
我们看到在tracegen.c文件中,是这样定义矩阵A和B的空间的:
1 2 static int A[256 ][256 ];static int B[256 ][256 ];
我们看到两个矩阵是连续分布的,首地址相隔256 × 256 × 4 = 2 18 256 \times 256 \times 4 = 2^{18} 256 × 256 × 4 = 2 18 A和B的首地址的index是相同的,即会映射到同一个缓存组,因此可能会造成冲突。
再看是如何实现不同大小的数组表示的,我们看cachelab.c里面是怎么写的,例如初始化数据的方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 void initMatrix (int M, int N, int A[N][M], int B[M][N]) { int i, j; srand(time(NULL )); for (i = 0 ; i < N; i++) { for (j = 0 ; j < M; j++) { A[i][j] = rand(); B[j][i] = rand(); } } }
是直接通过指定传入的数组的行列维数来对内存中的数据进行操作的,取出的对应的数据的偏移量是按照新给出的行列算出的,因此数组仍然是连续空间,这点不用担心。
使用介绍
填写代码
我觉得出题者写题目构成的程序就写的很优雅,我们可以在trace.c文件中构造多个函数,但是以带有char transpose_submit_desc[] = "Transpose submission"的函数为准进行提交测试。
例如我们将最简单的变换方法也就是trans方法填进transpose_submit函数里:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { int i, j, tmp; for (i = 0 ; i < N; i++) { for (j = 0 ; j < M; j++) { tmp = A[i][j]; B[j][i] = tmp; } } }
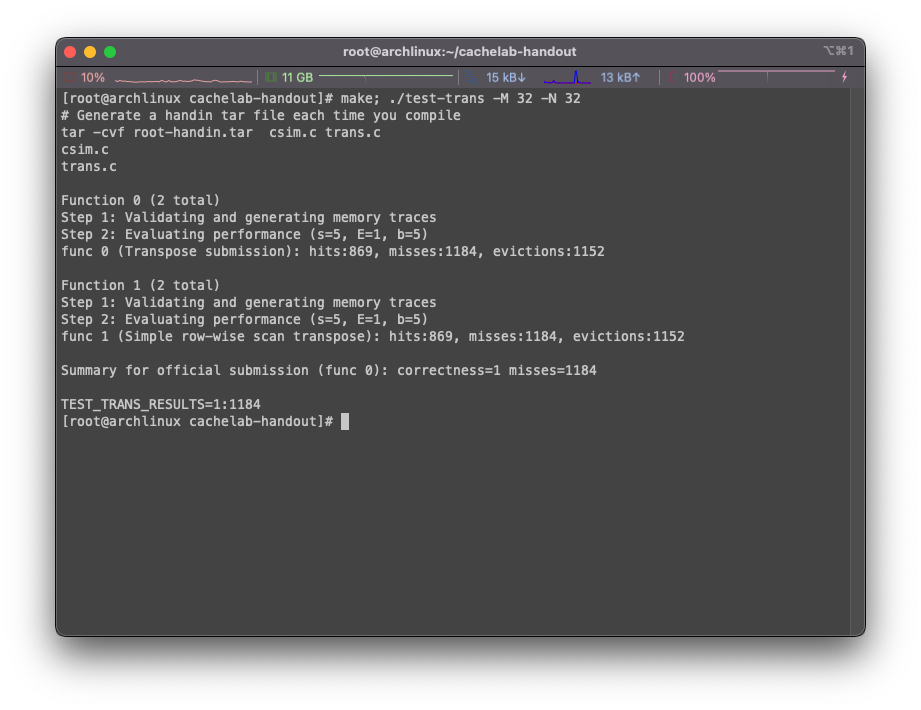
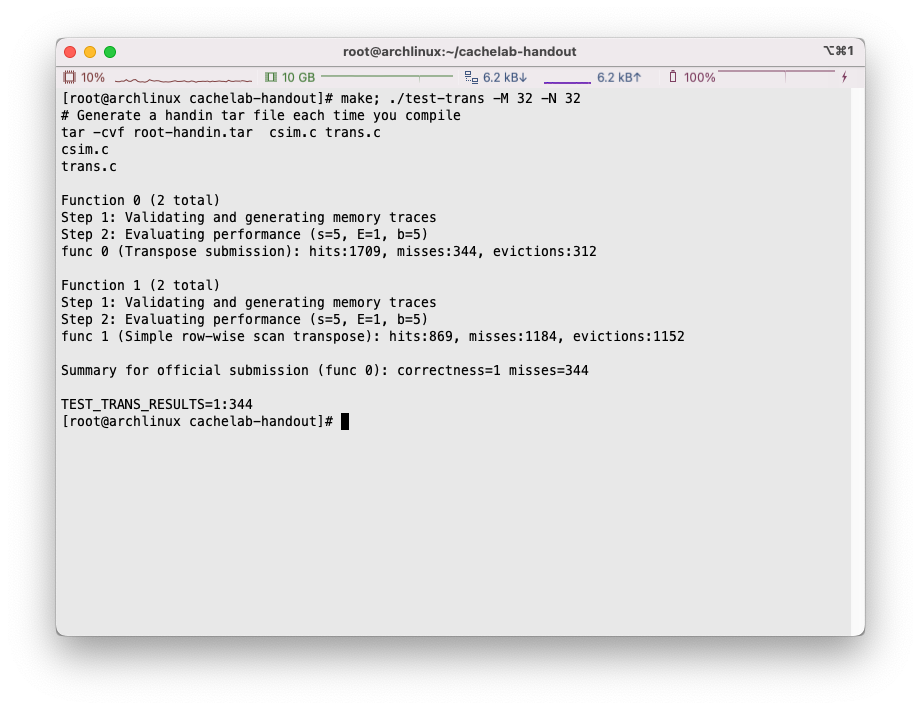
随后执行make; ./test-trans -M 32 -N 32:
可以看到程序针对trans.c中的两个方法分别进行了分析,在示例使用中,我们有提交函数transpose_submit(作为func 0)和trans函数(作为func 1)。
首先检查了方法的正确性,其次程序统计了发生miss的次数,这里没有做任何优化的情况下高达1184次,由于两个函数完全一致,两个函数的分析结果也一致,非常的合理。但是最终结果以提交函数func 0为准。
debug方法
纯看miss次数其实意义不大,更关键的是需要去寻找一个合理的办法进行debug。
在刚才我们调用test-trans时,在目录下程序自动生成了两个trace文件,分别代表了刚才的func 0和func 1:
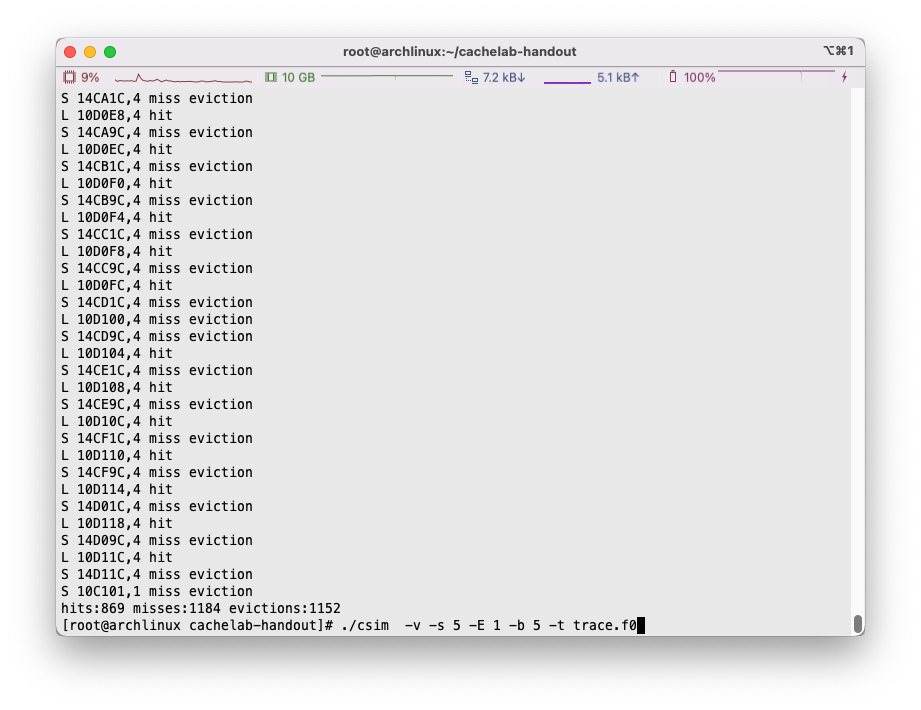
如果愿意,我们完全可以通过调用刚才完成的csim指令来查看具体是哪个位置发生了miss:
可能的冲突
矩阵内部冲突
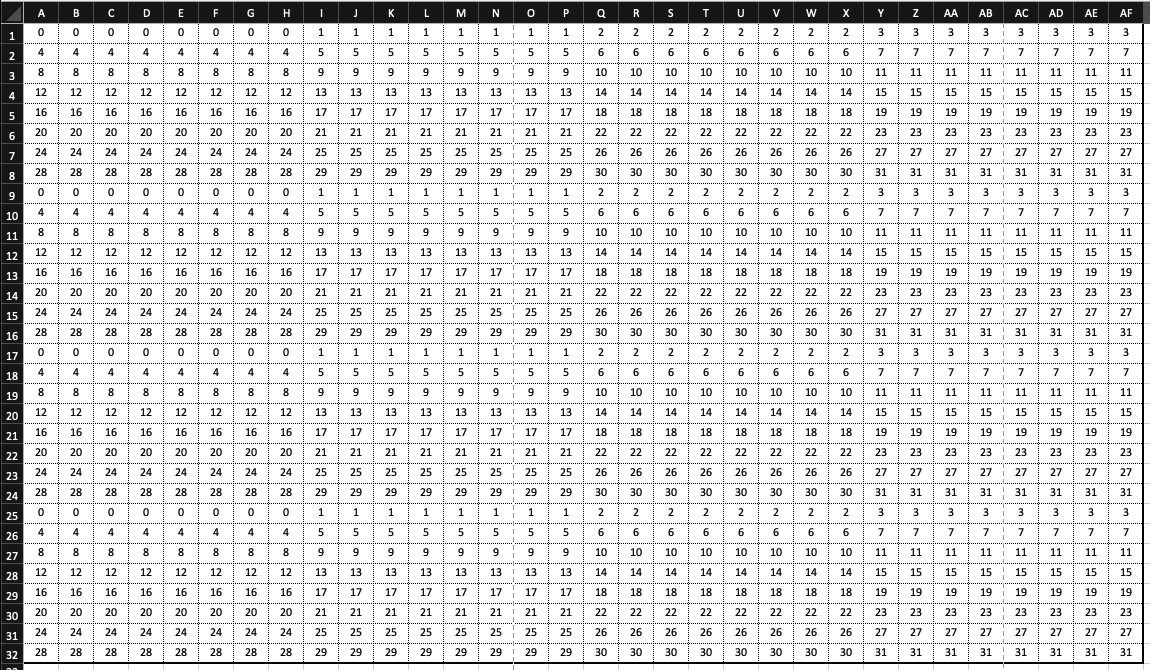
我们例如以第一题32 × 32 32 \times 32 32 × 32
例如可以看到加载[0][0~7]缓存和加载[8][0~7]缓存就有可能发生冲突,因为他们都被映射到了同一个缓存组中。
因此,例如当我们依次处理B[0][0~31] = A[0~31][0]时,会出现大量A矩阵内部的缓存冲突,如果需要不断的长距离遍历,miss次数会非常之多。同理,B矩阵也有可能会经历此类问题,也就是例如B[0~31][0] = A[0][0~31],也会出现非常多的miss。
这就带来了分块的概念了,我们需要将每次操作的范围限制在一个合理的区域内,方便我们充分利用缓存,尽量降低缓存可能发生的冲突。例如在上述情况下,我们使用一个8 × 8 8 \times 8 8 × 8
关于分块,非常有借鉴意义的就是CS:APP在官网上贴出的学习资料了:
CS:APP2e Web Aside MEM:BLOCKING: Using Blocking to Increase Temporal Locality
觉得英文累的小伙伴可以看这份:
网络旁注:使用分块技术提高时间局部性
矩阵之间冲突
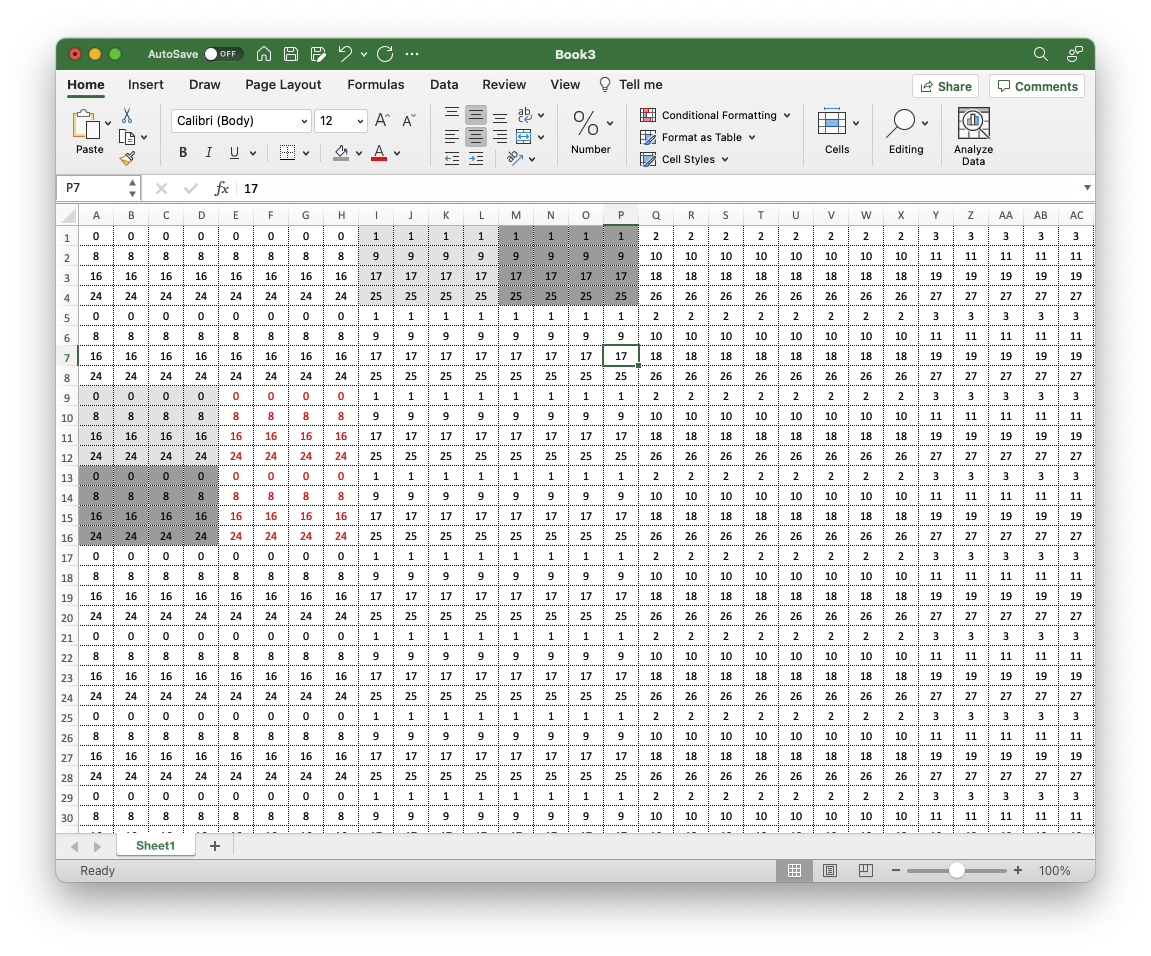
刚才我们已经提到了A和B矩阵的大小相比缓存大小非常巨大,且A和B矩阵首地址会映射到同一个缓存组上。以32 × 32 32 \times 32 32 × 32
例如B[0][0] = A[0][0]时,我们首先会先去加载A[0][0]也就是将A[0][0~7]加入缓存中,接下来又需要访问B[0][0],需要将B[0][0~7]加载进入缓存,这个时候由于映射的缓存组相同,就会发生很明显的冲突。同理,在[1][1],[2][2]…等位置也会发生这样的情况。
为了解决这样的问题,我们需要引入临时变量(寄存器),通过暂时存储的方式,打乱原先的读写节奏,来达到减少冲突miss的效果。
题目
32 x 32矩阵转置
根据刚才的描述,我们大致可以得到结论,即使用8 × 8 8 \times 8 8 × 8
也就是:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { for (int i = 0 ; i < 32 ; i += 8 ){ for (int j = 0 ; j < 32 ; j += 8 ){ for (int m = i; m < i + 8 ; m++){ for (int n = j; n < j + 8 ; n++){ B[n][m] = A[m][n]; } } } } }
我们看到通过这样的操作,miss的数量显著下降了:
miss数量从1184次下降到了344次,但是还不满足预期需求。
接下来,我们考虑通过使用临时变量的方式,打乱读取和写入的节奏,看看能否减缓矩阵之间发生的冲突。
例如,在将A[0][0~7]写入到B[0~7][0]的过程中时,首先加载A[0][0]发生cold miss,接下来加载B[0][0]由于映射到了相同的缓存组,会导致冲突miss,接下来加载A[0][1]时又需要再次加载到缓存,又是一次冲突,miss,效率大大下降,接下来加载B[1][0], B[2][0] …的时候各会发生一次cold miss,但是A[0][2], A[0][3]…进行访存的时候由于已经在缓存中了就不会发生冲突了,因此共计会发生10次miss。接下来遍历各行时,冲突次数会稍稍减少,但是对角线上仍然会发生miss。
我们选择一次性读取一行的内容,比如我们一次性把A[0][0~7]计入到x0, x1, x2, …, x7中,再一次性写到B[0~7][0]中,这样我们就不会在反复横跳中不断发生冲突miss了。
可以想像到的是这类的冲突只会发生在对角线所处的8 × 8 8 \times 8 8 × 8
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { for (int i = 0 ; i < 32 ; i += 8 ) { for (int j = 0 ; j < 32 ; j += 8 ) { for (int m = i; m < i + 8 ; m++) { if (i == j) { int x0 = A[m][j]; int x1 = A[m][j + 1 ]; int x2 = A[m][j + 2 ]; int x3 = A[m][j + 3 ]; int x4 = A[m][j + 4 ]; int x5 = A[m][j + 5 ]; int x6 = A[m][j + 6 ]; int x7 = A[m][j + 7 ]; B[j][m] = x0; B[j + 1 ][m] = x1; B[j + 2 ][m] = x2; B[j + 3 ][m] = x3; B[j + 4 ][m] = x4; B[j + 5 ][m] = x5; B[j + 6 ][m] = x6; B[j + 7 ][m] = x7; } else { for (int n = j; n < j + 8 ; n++) { B[n][m] = A[m][n]; } } } } } }
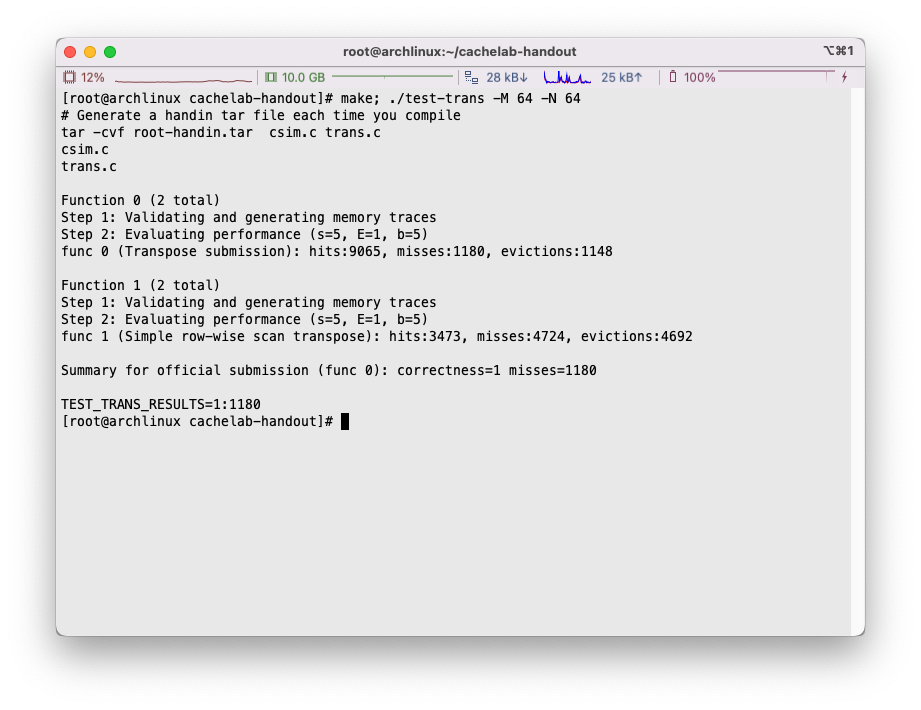
现在miss的数量下降到了288个,已经满足要求了:
我们现在再思考一下,剩下的冲突miss主要是由于什么原因触发的。很显然,B矩阵的8 × 8 8 \times 8 8 × 8 A矩阵的访问会导致B矩阵部分缓存的换出,而被换出的B矩阵部分需要再重新加载回来。这样下来的话,不考虑cold miss的话,平均8 × 8 8 \times 8 8 × 8
有一种挺反直觉的办法,我们可以直接将A矩阵8 × 8 8 \times 8 8 × 8 B矩阵中去。例如,我们每次将A[0][0~7]复制到B[0][0~7]中,当然也要通过临时变量,这样的话平均下来每行的冲突miss开销只有将A中一行缓存行替换成B中的一次开销。最后我们再针对复制完成的B矩阵8 × 8 8 \times 8 8 × 8 B的缓存了,因此没有miss冲突。
我们的开销只有A[0][0~7] -> B[0][0~7], A[1][0~7] -> B[1][0~7], …, 共8次。
代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { int x0, x1, x2, x3, x4, x5, x6, x7, i, j, t, k; for (i = 0 ; i < 32 ; i += 8 ) { for (j = 0 ; j < 32 ; j += 8 ) { for (t = 0 ; t < 8 ; t++){ x0 = A[i + t][j]; x1 = A[i + t][j + 1 ]; x2 = A[i + t][j + 2 ]; x3 = A[i + t][j + 3 ]; x4 = A[i + t][j + 4 ]; x5 = A[i + t][j + 5 ]; x6 = A[i + t][j + 6 ]; x7 = A[i + t][j + 7 ]; B[j + t][i] = x0; B[j + t][i + 1 ] = x1; B[j + t][i + 2 ] = x2; B[j + t][i + 3 ] = x3; B[j + t][i + 4 ] = x4; B[j + t][i + 5 ] = x5; B[j + t][i + 6 ] = x6; B[j + t][i + 7 ] = x7; } for (t = 0 ; t < 8 ; t++){ for (k = t + 1 ; k < 8 ; k++){ x0 = B[t + j][k + i]; B[t + j][k + i] = B[k + j][t + i]; B[k + j][t + i] = x0; } } } } }
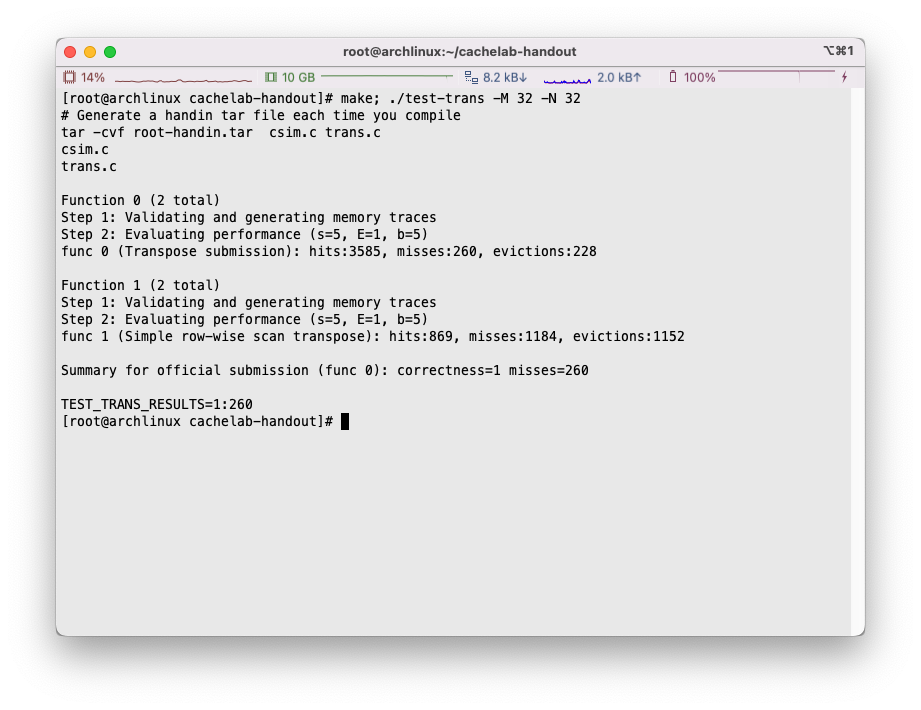
P.S. 注意,原地翻转数组的时候只要遍历上三角或者下三角区域即可😅完全遍历一遍相当于翻了又翻回来了
通过这么一番折腾,我们成功将miss数量减少到了260次:
64 x 64矩阵转置
64 × 64 64\times64 64 × 64
我们看到在纵向上,同矩阵内部[0][0~7]和[4][0~7]映射到了相同的缓存组,根据刚才的理解,我们这次分块应当选择4 × 4 4\times4 4 × 4
我们尝试如法炮制刚才的手段:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { int x0, x1, x2, x3, i, j, t, k; for (i = 0 ; i < 64 ; i += 4 ) { for (j = 0 ; j < 64 ; j += 4 ) { for (t = 0 ; t < 4 ; t++){ x0 = A[i + t][j]; x1 = A[i + t][j + 1 ]; x2 = A[i + t][j + 2 ]; x3 = A[i + t][j + 3 ]; B[j + t][i] = x0; B[j + t][i + 1 ] = x1; B[j + t][i + 2 ] = x2; B[j + t][i + 3 ] = x3; } for (t = 0 ; t < 4 ; t++){ for (k = t + 1 ; k < 4 ; k++){ x0 = B[t + j][k + i]; B[t + j][k + i] = B[k + j][t + i]; B[k + j][t + i] = x0; } } } } }
获得了大概1604次的miss:
还是没有达到我们希望的效果,猜测是由于4 × 4 4\times4 4 × 4 32字节,也就是8个int。我们很容易没法充分利用好后半段的缓存行。
例如:
当A矩阵可以一次进行[0][8]~[3][11]和[0][12]~[3][15]两数据块的访问,但是与此同时,B矩阵访问的却是[8][0]~[11][3]和[12][0]~[15][3]的部分,很显然右半块红色的缓存就没有被充分利用,而这带来了大量的冲突miss。
但是我们目前手头的局部变量非常有限,并没有什么很好的办法直接将一块4 × 4 4 \times 4 4 × 4
这里参考了深入理解计算机系统-cachelab ,这位佬的学习笔记,感觉非常有帮助。
我们可以考虑,使用8 × 8 8 \times 8 8 × 8 4 × 4 4 \times 4 4 × 4
我们按照如下的方式进行矩阵的处理:
根据佬的提示,尝试写出代码:
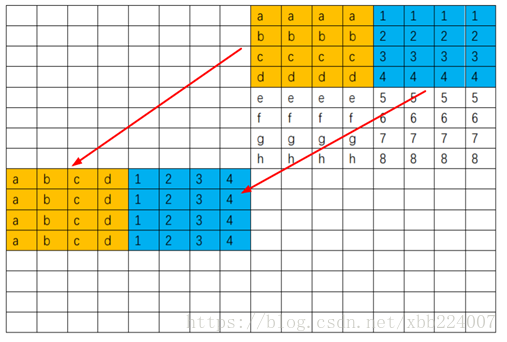
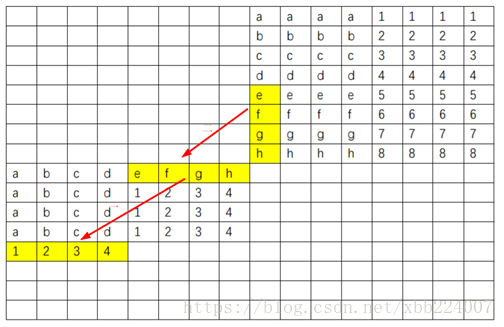
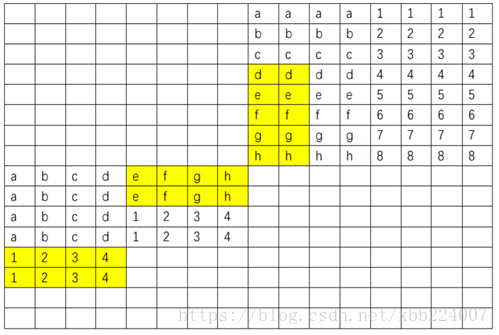
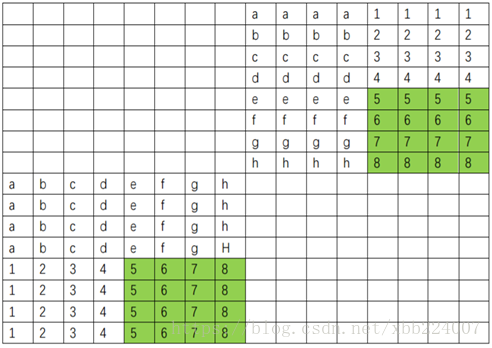
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { int i, j, m, n, x0, x1, x2, x3, x4, x5, x6, x7; for (i = 0 ; i < 64 ; i += 8 ) { for (j = 0 ; j < 64 ; j += 8 ) { for (m = i; m < i + 4 ; m++) { x0 = A[m][j]; x1 = A[m][j + 1 ]; x2 = A[m][j + 2 ]; x3 = A[m][j + 3 ]; x4 = A[m][j + 4 ]; x5 = A[m][j + 5 ]; x6 = A[m][j + 6 ]; x7 = A[m][j + 7 ]; B[j][m] = x0; B[j + 1 ][m] = x1; B[j + 2 ][m] = x2; B[j + 3 ][m] = x3; B[j][m + 4 ] = x4; B[j + 1 ][m + 4 ] = x5; B[j + 2 ][m + 4 ] = x6; B[j + 3 ][m + 4 ] = x7; } for (n = j; n < j + 4 ; n++){ x0 = A[i + 4 ][n]; x1 = A[i + 5 ][n]; x2 = A[i + 6 ][n]; x3 = A[i + 7 ][n]; x4 = B[n][i + 4 ]; x5 = B[n][i + 5 ]; x6 = B[n][i + 6 ]; x7 = B[n][i + 7 ]; B[n][i + 4 ] = x0; B[n][i + 5 ] = x1; B[n][i + 6 ] = x2; B[n][i + 7 ] = x3; B[n + 4 ][i] = x4; B[n + 4 ][i + 1 ] = x5; B[n + 4 ][i + 2 ] = x6; B[n + 4 ][i + 3 ] = x7; } for (m = i + 4 ; m < i + 8 ; m++){ x0 = A[m][j + 4 ]; x1 = A[m][j + 5 ]; x2 = A[m][j + 6 ]; x3 = A[m][j + 7 ]; B[j + 4 ][m] = x0; B[j + 5 ][m] = x1; B[j + 6 ][m] = x2; B[j + 7 ][m] = x3; } } } }
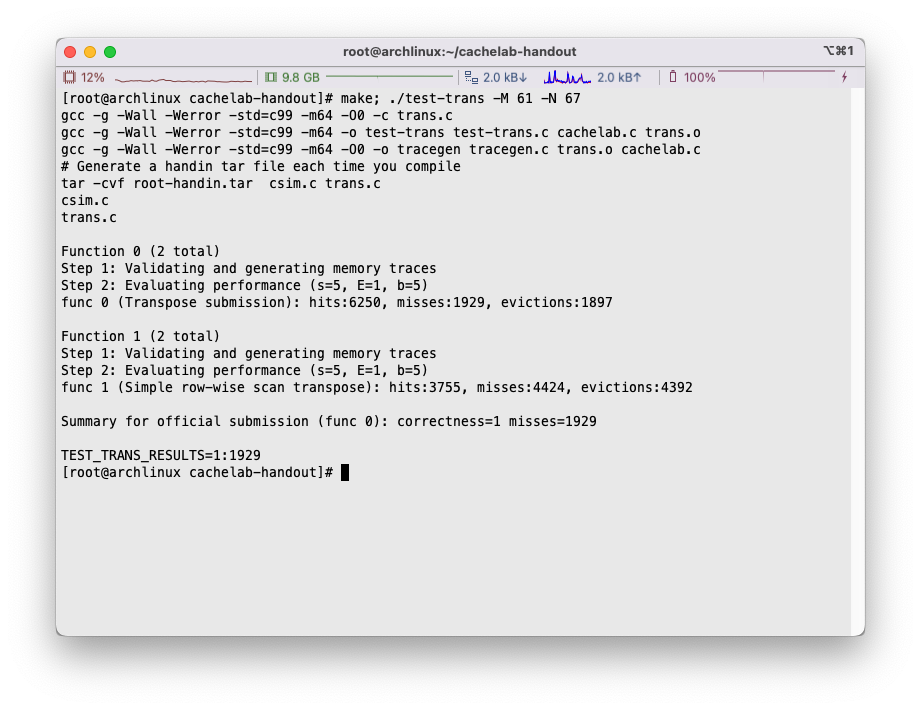
将miss数量降到了1180:
61 x 67矩阵转置
由于维数的不规则,导致内存空间映射到缓存上会非常的诡异。
我们就直接采用简单的分块策略进行分析即可,我们尝试不同的分块规模,形成下表:
分块规模
miss数量
2 × 2 2 \times 2 2 × 2 3116
3 × 3 3 \times3 3 × 3 2649
4 × 4 4 \times 4 4 × 4 2426
5 × 5 5\times5 5 × 5 2297
6 × 6 6\times6 6 × 6 2225
7 × 7 7\times7 7 × 7 2153
8 × 8 8\times8 8 × 8 2119
9 × 9 9\times9 9 × 9 2093
10 × 10 10 \times 10 10 × 10 2077
11 × 11 11 \times 11 11 × 11 2090
12 × 12 12 \times 12 12 × 12 2058
13 × 13 13\times13 13 × 13 2049
14 × 14 14\times14 14 × 14 1997
15 × 15 15\times15 15 × 15 2022
16 × 16 16 \times 16 16 × 16 1993
17 × 17 17 \times 17 17 × 17 1951
18 × 18 18\times18 18 × 18 1962
19 × 19 19 \times 19 19 × 19 1980
20 × 20 20\times20 20 × 20 2003
21 × 21 21\times21 21 × 21 1958
22 × 22 22\times22 22 × 22 1960
23 × 23 23\times23 23 × 23 1929
24 × 24 24\times24 24 × 24 2016
那么我们选择分块大小23 × 23 23\times23 23 × 23
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { int i, j, m, n; for (i = 0 ; i < 67 ; i += 23 ) { for (j = 0 ; j < 61 ; j += 23 ) { for (m = i; m < 67 && m < i + 23 ; m++) { for (n = j; n < 61 && n < j + 23 ; n++) { B[n][m] = A[m][n]; } } } } }
miss数量能够控制的比较合理:
总结
最后我们将transpose_submit方法整理一下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 char transpose_submit_desc[] = "Transpose submission" ;void transpose_submit (int M, int N, int A[N][M], int B[M][N]) { if (M == 32 && N == 32 ) { int x0, x1, x2, x3, x4, x5, x6, x7, i, j, t, k; for (i = 0 ; i < 32 ; i += 8 ) { for (j = 0 ; j < 32 ; j += 8 ) { for (t = 0 ; t < 8 ; t++) { x0 = A[i + t][j]; x1 = A[i + t][j + 1 ]; x2 = A[i + t][j + 2 ]; x3 = A[i + t][j + 3 ]; x4 = A[i + t][j + 4 ]; x5 = A[i + t][j + 5 ]; x6 = A[i + t][j + 6 ]; x7 = A[i + t][j + 7 ]; B[j + t][i] = x0; B[j + t][i + 1 ] = x1; B[j + t][i + 2 ] = x2; B[j + t][i + 3 ] = x3; B[j + t][i + 4 ] = x4; B[j + t][i + 5 ] = x5; B[j + t][i + 6 ] = x6; B[j + t][i + 7 ] = x7; } for (t = 0 ; t < 8 ; t++) { for (k = t + 1 ; k < 8 ; k++) { x0 = B[t + j][k + i]; B[t + j][k + i] = B[k + j][t + i]; B[k + j][t + i] = x0; } } } } } else if (M == 64 && N == 64 ) { int i, j, m, n, x0, x1, x2, x3, x4, x5, x6, x7; for (i = 0 ; i < 64 ; i += 8 ) { for (j = 0 ; j < 64 ; j += 8 ) { for (m = i; m < i + 4 ; m++) { x0 = A[m][j]; x1 = A[m][j + 1 ]; x2 = A[m][j + 2 ]; x3 = A[m][j + 3 ]; x4 = A[m][j + 4 ]; x5 = A[m][j + 5 ]; x6 = A[m][j + 6 ]; x7 = A[m][j + 7 ]; B[j][m] = x0; B[j + 1 ][m] = x1; B[j + 2 ][m] = x2; B[j + 3 ][m] = x3; B[j][m + 4 ] = x4; B[j + 1 ][m + 4 ] = x5; B[j + 2 ][m + 4 ] = x6; B[j + 3 ][m + 4 ] = x7; } for (n = j; n < j + 4 ; n++) { x0 = A[i + 4 ][n]; x1 = A[i + 5 ][n]; x2 = A[i + 6 ][n]; x3 = A[i + 7 ][n]; x4 = B[n][i + 4 ]; x5 = B[n][i + 5 ]; x6 = B[n][i + 6 ]; x7 = B[n][i + 7 ]; B[n][i + 4 ] = x0; B[n][i + 5 ] = x1; B[n][i + 6 ] = x2; B[n][i + 7 ] = x3; B[n + 4 ][i] = x4; B[n + 4 ][i + 1 ] = x5; B[n + 4 ][i + 2 ] = x6; B[n + 4 ][i + 3 ] = x7; } for (m = i + 4 ; m < i + 8 ; m++) { x0 = A[m][j + 4 ]; x1 = A[m][j + 5 ]; x2 = A[m][j + 6 ]; x3 = A[m][j + 7 ]; B[j + 4 ][m] = x0; B[j + 5 ][m] = x1; B[j + 6 ][m] = x2; B[j + 7 ][m] = x3; } } } } else if (M == 61 && N == 67 ) { int i, j, m, n; for (i = 0 ; i < 67 ; i += 23 ) { for (j = 0 ; j < 61 ; j += 23 ) { for (m = i; m < 67 && m < i + 23 ; m++) { for (n = j; n < 61 && n < j + 23 ; n++) { B[n][m] = A[m][n]; } } } } } }
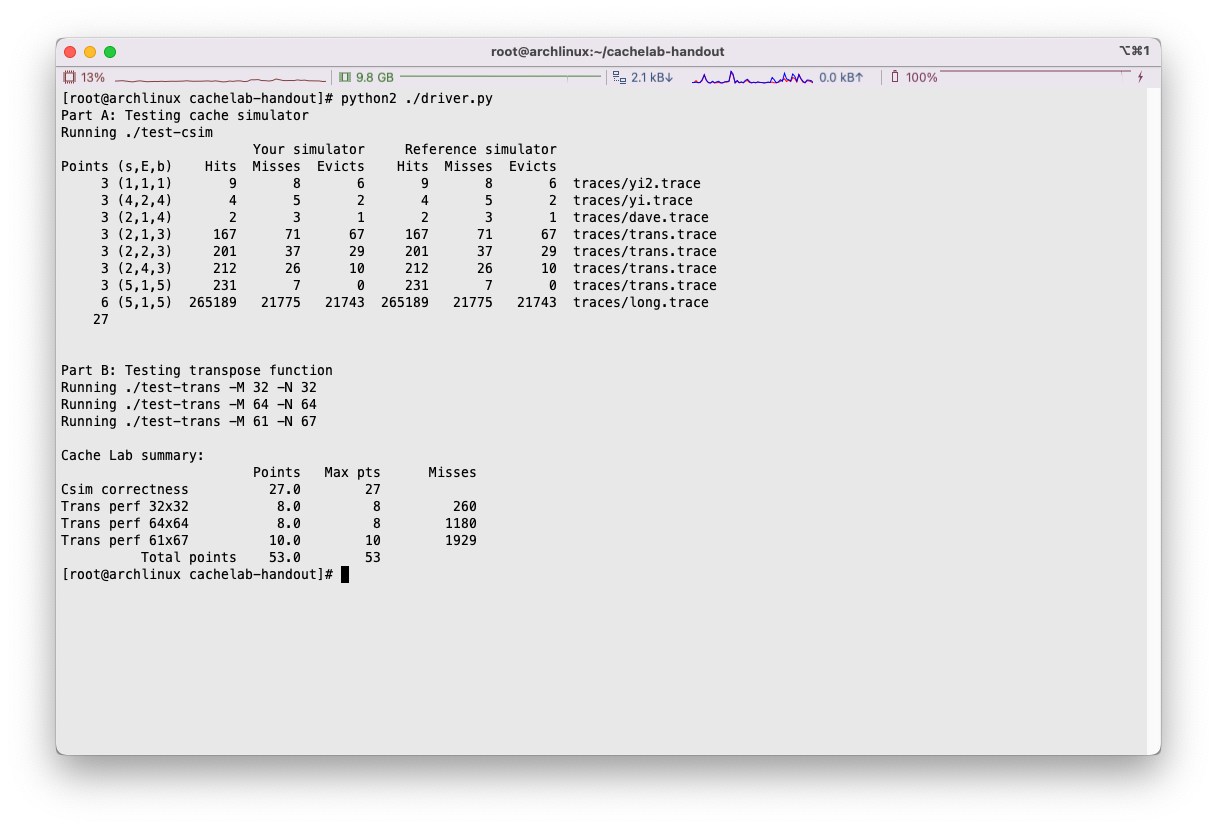
运行./driver.py,即可对整次的lab进行评分,注意要使用Python2:
痛苦面具了属于是,总而言之,好难啊~
书里讲的内容很基础,老师上课讲的也是很基础,还是重在理解吧。
通过这次的Lab,我对缓存有了更加进一步的认识,了解了如何调整代码通过提升程序的时间和空间局部性,来尽量减少缓存未命中的次数。